Tartalom:
- Arduino analóg bementének használatával egyenfeszültség minimum, maximum, középérték, valódi effektív érték, periódusidő és frekvencia valamint kitöltéséi tényező mérése egyszerre.
- Tetszőleges periódikus jelalakkal elboldogul, ami nem nagyon zajos.
- 4Hz-től és 500Hz-1Khz maximális jelfrekvenciáig működik.
- A mérési (kijelzési) gyakoriság a jel frekvenciájától függ, maximum 1-2 másodperc.
- A működés oszcilloszkóppal ellenőrzött folyamatának leírása szinusz, háromszög és négyszög jelekkel
——————————————————————————————————————
Az amatőr gyakorlatban nagyon ritkán van szükség igazán pontos merőműszerre. Vettem magamnak 20.000Ft-ért egy szuper 4 számjegyes mérőműszert (HP760H). Automatikus méréshatár váltás, frekvencia és hőmérséklet mérés ellenállás és kapacitás mérés stb. mind benne van. A gyakorlatban azonban még soha nem volt szükségem ilyen pontosságra és funkciókra. Frekvenciát talán egyszer mértem vele, hőmérsékletet is csak egyszer-kétszer, de rá kellett jönnöm, hogy az egész fokokban történő kijelzés miatt ez sem használható sok mindenre. Alkatrészek bevizsgálására sokkal hatékonyabb egy célműszer. Szóval egy amatőrnek nem kell ilyen sok minden, nem kell ennyit költeni. Gondolkodni kezdtem, hogy mire is lenne szükségem a kényelmesebb munka érdekében, és arra jutottam, hogy nem a pontosság, hanem a mért jel minél több paraméterének az egyszerre történő kijelzése lenne inkább hasznos. Abból indultam ki, hogy jellemzően 0-30V körüli egyenfeszültségekkel dolgozom, főleg 5 és 12V-al, és az esetlegesen változó jelek frekvenciája is 1Khz alatti. Természetesen sokkal nagyobb frekvenciák is vannak környezetemben, pl. az Arduino órajel 16Mhz, de azt nem szoktam megmérni. Ezek alapján a legfontosabb jellemzők az éppen mért jel minimuma, maximuma, frekvenciája (periódusideje), kitöltési tényezője. Eszembe jutott az effektív érték is, bár arra elég ritkán van szükségem. Esetleg, amikor teljesítmény led-ek fényerőszabályozásával foglalkozom, ez is szóba kerülhet. Ugyanakkor pont az effektív érték az, ami kihívást jelent, így ezt jelöltem meg a fő célként, amúgy csak virtusból!
Vannak egyéb kényelmi szempontjaim is, ami miatt egy saját mérőműszer építésébe kezdenék. Pl. csak szakadás vizsgálat esetén sípol a méregdrága luxus multiméterem, de nem állítható be hanghatás egy konkrét feszültség értékre. Pedig a hangjelzés máskor is jó lenne. Pl. ha nagy nehezen megkeresem az áramkörben a megfelelő pontot, és oda ügyeskedem a műszer érintkezőjét, a műszerre tekintéssel egy esetleges rövidzár okozást kockáztatok. Általában nem az érdekel, hogy a feszültség pontosan mennyi, elég lenne tudni, hogy 5V vagy nulla. Ehhez hasonló praktikus gondolatok kavarogtak a fejemben, amikor elindultam ezen az úton.
Egy mérőműszer készítése azonban kihívás. Legyen kisméretű, működjön elemről vagy akkumulátorról, nem kell, hogy precíziós legyen, de azért van egy elvárt pontosság is. Még nem biztos, hogy mindezeket meg tudom csinálni, de hozzákezdtem. Az első lépés a „jelfeldolgozó” algoritmus, ami megállapítja a fentiekben megadott fontos jel paramétereket. Az alább részletezett algoritmussal hetekig kísérleteztem. Mivel többé kevésbe sikeres volt ténykedésem, publikálásra alkalmas kísérletnek gondolom.
A legfontosabb bevezető kísérlet annak megállapítása volt, hány mérést is tud az Arduino Uno (ATmega328) csinálni. Ehhez egyszerű programot írtam, ami csak mér, és minden mérés után számol egy másodpercen keresztül. A végeredmény több mint 8000. A mintavételi törvény alapján ez kb. 4 Khz maximális frekvenciájú jel helyreállítását tenné lehetővé. Bár azt nem tudom, hogy ez egészen pontosan mit is jelent, de azt sejtem, hogy a maximum 0-1000Hz-s jelek tartományában a 8000 mintavétel jó lesz valamire, tehát van értelme elkezdeni a munkát. Tudvalévő, hogy az Arduino PWM kimenetének alapértelmezett frekvenciája 500Hz körüli. A 230V egyenirányításával nyert szűretlen egyenfeszültség meg 100Hz, tehát valamire jó lehet, egy ennyire szerény képességű műszer is.
A minimum és a maximum meghatározása egyáltalán nem nagy feladat. A frekvencia és a periódus idő megméréséhez azonban már elegendő pontossággal meg kell állapítani a minimum és maximum helyek, vagy a jelfelfutási pontok helyét. Bár jellemzően négyszög jelekre számítok, előfordulhat szinusz jel is. Pl. ha egy graetz egyenirányító kimenetén akarom a feszültséget megmérni. Kezdetben azzal kísérleteztem, hogy megpróbáltam a minimum és maximum helyeket megkeresni. Elvben egyszerű, amikor egy jel csökkenni kezd, akkor az előző mérés a maximum. Sajnos azonban a jelek lehetnek zajosak. Ráadásul a csökkenés újra növekedés követheti, és egy pillanat alatt olyan bonyolult lesz a helyzet, amit így nem lehet követni program algoritmussal. A kitalált megoldásom végül is nagyon egyszerű. Egy konkrét ideig tartó méréssel (ez 250msec lett) megkeresem a minimális és a maximális feszültséget. Ha legalább egy teljes periódus belefért ebbe az időszakba, akkor ez az idő elegendő. Ekkor a felbontás segít, hiszen 2000 mérési adat áll rendelkezésre, ebből kell a minimális és a maximális számadat. Vagyis algoritmusom elméleti minimális frekvenciája 4Hz (250msec periódus idő). A maximális frekvencia 4khz-ig bármi lehet, hiszen olyan sok minimum és maximum hely lesz 250msec alatt egy 4khz-s jelnél, hogy statisztikailag nagy valószínűséggel rá fogok találni a minimumra és a maximumra is. Itt még nem érdekes, hogy hol van a minimum és a maximum, csak az, hogy mennyi!
Ha már tudom a minimumot és a maximumot, akkor felosztom a feszültség tartományt három egyenlő részre. Miért egyenlő részekre? Csak! Azzal a feltételezéssel élek, hogy a jel többé kevésbé egyenletesen fog változni, tehát nem lesznek kiugróan nagy perióduson belüli kilengések. Így fogom elkülöníteni a minimum és a maximum helyek környezetét. Nézzük meg ábrán is, hogy mi a működési elv alapja:
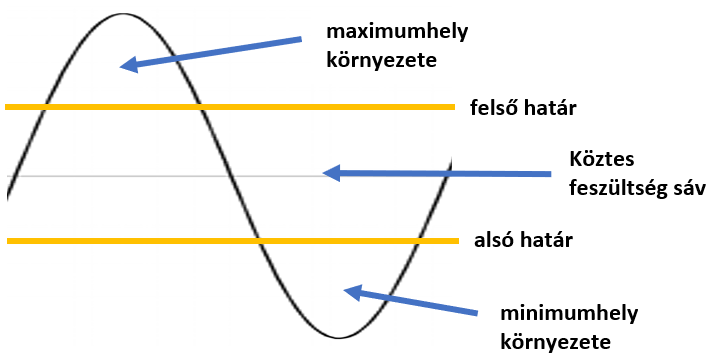
A középső köztes sáv feladata, hogy elkülönítse a minimum és maximum helyeket. Az algoritmusom meg fogja állapítani, ha a jel a maximumhely környezetében tartózkodik. Akkortól tekintjük maximum helynek amikor egy felső határ feletti mérés érkezik. Ezt követően ha zajos a jel, akkor lehet, hogy a köztes sávból is érkeznek mérések, de addig nincs baj, amíg az alsó határból nem érkezik mérési eredmény. Tehát ha a zaj kisebb, mint a minimum és maximum közötti feszültség harmada, akkor jól állapítottam meg azt, ha a jel a maximum pontján vagy annak közelében tartózkodik. Ezt követően azt kell figyelnem, hogy mikor érkezik az alsó határ alatti feszültség, ez ugyanis a minimumhely kezdetét fogja jelenteni. Itt a sorrend fontos, tehát először megvárok egy maximum helyet, megjegyzem, hogy volt maximumhelybe tartozó feszültség, és addig várok, amig minimumhelybe tartozó feszültség meg nem érkezik. A periódus kezdő pontja ekkor az a pillanat, amikor az első olyan feszültséget mérem, ami alsó határnál kisebb. Ugyanígy keresem meg a következő periódus kezdő pontját is. Lehetne pont fordítva is, tehát először keresek egy minimumhelyet, és a maximum hely kezdetét határozom meg. Történelmileg alakult így, mint a jobb oldali közlekedés. Biztos kevesen tudják, hogy a gödöllői hév építésekor még nem döntötték el, hogy jobb, vagy baloldali közlekedés lesz hazánkban. Így a gödöllői hév mai napig a bal oldali sínpáron halad, jól megzavarva az idegeneket, akik mindig a másik oldali peronon várakoznak. Így esetleg zavaró módon, de a minimum hely kezdetével számítom a periódusidőt, és nem a maximumhellyel! Egyébként meg mindegy!
Mivel a jelalakról semmit nem tudok, akár zajos is lehet, több periódust érdemes átlagolni, és abból számítani a periódusidőt. Egy kis zajt tartalmazó jelnél láthatóan elkülöníthetők a minimum és maximum helyek:
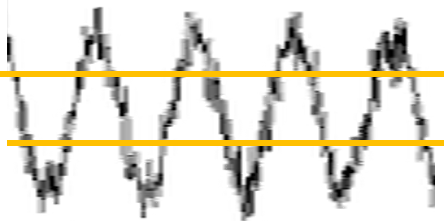
Nagy zaj esetén azonban már nem lehet ezzel az algoritmussal dolgozni. Nézzük példának ezt a jelet:
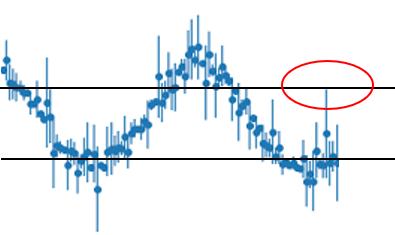
Látható, hogy időnként a minimum tartományból is átlóg jel a maximum tartományba, amit az algoritmusom úgy értékelne, hogy a minimum után elkezdődött egy maximum hely körüli szakasz, tehát egy teljes periódusnak értékelné a következő minimum határ alatti feszültséget.
A legpontosabban a négyszögjel periódus idejét lehet majd mérni, hiszen ott a jel gyakorlatilag a minimum és maximum között ugrál a középső sáv kihagyásával, így a periódusidő mérések időpillanata nagyon pontosan megállapítható.
Ezzel az algoritmussal, szándékozom tehát megmérni a minimum és maximum feszültséget, a periódusidőt, és ebből kiszámítható a frekvencia.
Hogyan lehetne kiszámítani a kitöltési tényezőt? Erre is egy nagyon egyszerű módszert találtam ki. Számolom a felső határ feletti, az alsó határ alatti és a köztes sávban is a mérések (mintavételek) darabszámát. Feltételezve, hogy két mintavétel között azonos idő telik el, a felső határ feletti és az alsó határ alatti mérések aránya a kitöltési tényezőt adja meg. Természetesen rontja a helyzetet, hogy nem tudjuk mi történik a köztes sávban, de ha azzal a feltételezéssel élünk, hogy ebben a tartományban nagyjából egyenletes jelmeredekséggel változik a feszültség, akkor a legegyszerűbb jelalakokra is jó lesz a képzett arányunk. Pl. szinusz szerű és háromszög jel esetén is lesz értékelhető jelentése a kitöltési tényezőnek. Mindazonáltal ezekre a jelalakokra nem sok értelme van a kitöltési tényezőt számolni. Négyszög jel esetén meg nincs gond, hiszen jó esetben a köztes sávból nem is lesz mérési eredményünk, mert a jelmeredekség sokkal nagyobb annál, hogy pont beletrafáljunk egy mintavétellel. Az Arduino kimenet négyszögjel felfutási ideje nanoszekundumos nagyságrend, miközben ennek többszázszorosa a két mintavétel között eltelt idő.
Van-e értelme az effektív érték mérésnek?! Naná! Kihívás megcsinálni, hiszen a valódi effektív érték mérő készülékek nagyon drágák (120ezer-nél kezdődnek). Az olcsó multiméterek (és itt az én 20.000Ft-os méregdrága mérőmüszerem is olcsónak számít) nem a valódi effektív értéket mérik. Feltételezik a műszer gyártók, hogy szinusz feszültséget fogunk mérni (vagyis a hálózati váltakozó feszültséget), megmérik a feszültség csúcsot, és elosztják gyök kettővel. Szinusz esetén ennyi az összefüggés. Ezek a műszerek azonban négyszögjelre már nem adnak valós effektív feszültséget.
(ennek a leírásnak a készítése után találtam egy mérőműszert az aliexpressen 3000Ft-ért, ami TrueRMS mérő, tehát máris elavultam https://www.aliexpress.com/item/1005001890547686.html?spm=a2g0s.8937460.0.0.7dd52e0eST1TnQ )
Az effektív érték mérés elve nem túl bonyolult. A definíció szerint az effektív érték az az egyenfeszültség-szint vagy egyenáram-áramerősség, amely átlagosan ugyanakkora Joule-hőt termel egy ellenálláson. A hőtermelés arányos a teljesítménnyel, ami a feszültség és áram szorzata. Egy ellenálláson folyó áram arányos a feszültséggel, így a teljesítmény egy négyzetes mennyiség. Kis gondolkodás után belátható, hogy valójában a szinusz-négyzet függvény alatti területről van szó. Integrálni már rég nem tudok, de remélhetőleg nem is kell majd.
Egy teszőlegesen kicsire választott időegység alatt elvégzett munka (azaz a termelt hőmennyiség) az áram és feszültség szorzata szorozva az idővel. Természetesen ekkor azt feltételezzük, hogy jel nem változik lényegesen a választott kicsi időintervallumon belül, különben a jelelak ismeretében integrálni kellene, ezt meg már én nem tudok, mint említettem. Ha az eltelt idő végtelenül kicsi, akkor a pillanatnyi teljesítményt kapjuk meg, ami egyszerűen csak a pillanatnyi feszültség és a pillanatnyi áram szorzata. Hogy világosan érthető legyen, nézzünk egy egyszerű példát. Legyen egy négyszög jelünk, aminek 50%-os a kitöltése, 1V feszültség hatására 1A áram folyik a vezetékben, tehát az 1ohm-os ellenállásunkon amikor folyik rajta áram, 1 Watt teljesítmény alakul hővé, és szerencsénkre a négyszögjel esetén nem is változik a feszültség nagysága, amíg a négyszög „van feszültség” szakaszában járunk. Az egyszerűség kedvéért legyen a periódus idő 1 sec. Tehát ez a jelünk fél másodpercig van, fél másodpercig meg nincs. Mennyi munkát végez ez összesen 1 másodperc alatt? Hát pontosan 1V*1A*0.5sec=0,5Wsec munka végződik el. Ne zavarjon meg senkit, hogy a munkát inkább wattórában szokták megadni, ez most wattszekundumban is jó lesz. Mekkora egyenfeszültség végezne ugyanennyi munkát? Ez most nagyon egyszerű, mert a feszültség és áram szorzatának egy sec alatt 0,5W munkát kell végeznie, tehát x*x=0,5. Ebből következik, hogy x az gyök 0.5. Gyök 0,5 pedig 0,707. Ellenőrizzük is le: 0,707V*0,707A=0.5W. Ugye milyen meglepő? Megérzésből azt vártam volna, hogy pontosan 0,5V feszültség termelne ugyanannyi hőt, hiszen az pont fele. De nem, az effektív érték becsapós. Ha elővesztek egy táblázatot a különböző jelalakok effektív értékére, akkor ezt találjátok:
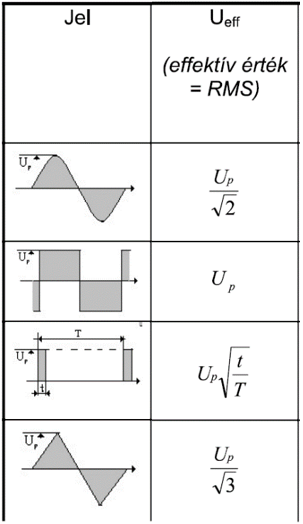
Ebben a táblázatban az Up a feszültség csúcsértéke. Le is ellenőrizhetnénk a táblázatból az előbbi számítást. A négyszögjelünk csúcsértéke azaz Up=1V. A képletből t=0,5, T=1. Tehát az effektív érték 1*gyök(0,5/1)-el egyezik meg. Bocs, de nem tudom jelekkel kiírni. Az eredményünk itt is 0,707, tehát jól számoltunk megérzésből, mert ezt erősítette meg a táblázatban szereplő képlet is. Most nézzük meg, mi történik, ha az Arduino egyik kimenetére ellenállást kapcsolunk, és PWM jellel hajtjuk meg. Legyen a kitöltési tényező a minimális, vagyis a 256 ciklusból csak egy alaklommal adunk a kimenetre 5V-ot. Ekkor az effektív értéke 5V*gyök(1/256)=0,0625V. Tehát ez az ellenállás annyi hőt fog termelni ennek a négyszögjelnek a hatására, mintha 0,0625V-ot kapcsoltunk volna rá.
Íme a program, ami a fenti mérési eredményeket megvalósítja:
int fesz; //egy mintavétel feszültsége
int feszmax=0; //egy mintavétel sorozatban a maximum érték
int feszmin=1023; //egy mintavétel sorozatban a minimum érték
long idotmp=millis(); //a minimum és maximum érték meghatározáskor, illetve a periódusidő mérésben használt segéd változó
long idotmp1=micros(); //a minimum és maximum érték meghatározáshoz használt változó másodpercenkénti törléséhez használt segéd változó
int minimum_db=0; //a minimum helyek darabszáma a jelalak mintavételeiből kimutatva
int alsohatar; //a minimumhelyek meghatározásához a minimum és maximum érték különbségéből kiszámolt feszültség érték.
//Ez alatti feszültség esetén azt feltételezzük, hogy a jel egy minimum hely közelében van, és ezeket a minimum helyeket akarjuk megszámolni
int felsohatar; //A maximum helyek meghatározásához a minimum és maximum érték különbségéből kiszámolt feszültség érték.
//Tudnunk kell, hogy mikor van a jel a maximum közelében, mert csak a maximumból a minimum felé haladva
//legelőször előforduló alsó határnál kisebb feszültségnél akarjuk elindítani a periódusidő mérést, és következő ciklusokban a mérés leállítását.
//Enélkül pontatlan lesz az időmérés (a minimum környezetében bárhol elindulhat a mérés amikor először belemegyünk a cilusba).
long minszam; //az alsó határ alatti feszültséget eredményező mintavételek száma abban az időszakban, amikor egész cilusok idejét mérjük
long maxszam; //az felső határ feletti feszültséget eredményező mintavételek száma abban az időszakban, amikor egész cilusok idejét mérjük
long koztesszam; //az felső és alsó határ közötti feszültséget eredményező mintavételek száma abban az időszakban, amikor egész cilusok idejét mérjük
byte start_jelzes=0; //azt a pillanatot jelzi, amikor megtaláltuk az első minimum hely elsó határ alatt feszültségét. Ekkor indul a periódusidő mérés valamint a kitöltési tényező mérés
bool minjelzo=0; //ez a változó jelzi, ha előfordult egy alsó határ alatti feszültség (a legelsőnél 1-re állítjuk)
bool maxjelzo=0; //ez a változó jelzi, ha előfordult egy felső határ feletti feszültség (a legelsőnél 1-re állítjuk)
float periodusido; //ebbe a változóba kerül több ciklus (jelenleg 5) periódus idejének átlaga
byte kitoltes; //a kitöltési tényező arányának százalékban megadott értéke. Csak az egész érték marad meg
int koztes_max; //az alsó és felső határ közötti mintavételek számának felosztásakor ebbe számoljuk ki, hogy mekkora részt tekintünk a köztes időszakból a maximum értékhez tartozónak
float frekvencia; //a frekvencia kiszámított értéke
float min_fesz; //a jel minimuma
float max_fesz; //a jel maximuma
float atl_fesz; //a jel átlaga
unsigned long gyujto; //a valódi effektív érték gyűjtéséhez a mintavételek négyzetének gyűjtője
float eff_fesz; //a jel számított effektív értéke
int kamu_i; //csak azonos mérési időkhöz, nincs valós tartalma a változónak
bool kamu_b; //csak azonos mérési időkhöz, nincs valós tartalma a változónak
void setup() {
Serial.begin(115200); //Soros port inicializálás
Serial.println("Indul..."); //indul a mérés
pinMode(3,OUTPUT); //négyszögjel kimenetnek használt kivezetés (csak négyszögjel vizsgálatnál)
analogWrite(3,15); //négyszögjel vizsgálatnál a 3. kivezetést használtam, változtattam a kitöltési tényezőt
analogReference(DEFAULT); //A tápfeszt veszi referenciának (5V) az ADC
}
void loop() {
idotmp=millis()+250; //250 msec-ig fogjuk keresni a minimum és a maximum értékét
do { //ez a ciklus állapítja meg az előforduló minimális és maximális feszültséget
fesz=analogRead(A0); //az A0 bemeneten végzünk egy mérést
if (fesz<feszmin) {feszmin=fesz;} //eddigi legkisebb feszültség keresése, tárolása
if (fesz>feszmax) {feszmax=fesz;} //eddigi legnagyobb feszültség keresése, tárolása
} while (idotmp>millis()); //ha még nem telt le a 250msec, akkor megy újra a ciklus
alsohatar=feszmin+((feszmax-feszmin)/3); //a minimum és maximum feszültség különbségének alsó harmada egy alsó határ feszültség
felsohatar=feszmax-((feszmax-feszmin)/3); //a minimum és maximum feszültség különbségének alsó felső egy felső határ feszültség
//Az alső és felső határ feszültség alatti feszültségek a periódus és a frekvencia meghatározáshoz kellenek
minjelzo=0; //ez a változó bebillen 1-re, amikor a mért feszültség az alsó határt átlépi (kisebb az alsó határnál)
maxjelzo=0; //ez a változó bebillen 1-re, amikor a mért feszültség az felső határt átlépi (nagyobb az felső határnál)
minimum_db=0; //nullázzuk az érzékelt minimumhelyek számát
start_jelzes=0; //ebben a változóban jelezzük, ha elindult a periódusidő mérése egy felderített minimumhelynél
kamu_i=0;
do { //ez a ciklus keresi meg és megszámolja a minimumhelyeket a jelalakban
fesz=analogRead(A0); //az A0 bemeneten végzünk egy mérést
gyujto=gyujto+((long)fesz*fesz); //effektív érték számításhoz gyűjtjük a mintavételi értékek négyeztét
//long-ra kell alakítani a fesz*fesz értékét, különben automatikusan int-re számolja ki,
//ami jelen esetben akár negatív érték is lehetne enélkül (előjeles az int)
if (fesz>felsohatar) {maxszam++;maxjelzo=1;} //számolunk, ha a mért feszültség a felső határ felett van
else {kamu_i++;kamu_b=1;} //csak azért kell, hogy az if és az else ágak végrehajtási ideje nagyából azonos legyen
if (fesz>alsohatar and fesz<felsohatar) {koztesszam++;} //számolunk, ha a mért feszültség az alsó és felső határ között van
else {kamu_i++;} //csak azért kell, hogy az if és az else ágak végrehajtási ideje nagyából azonos legyen
if (fesz<alsohatar) {minszam++;minjelzo=1;} //számolunk, ha a mért feszültség az alsó határ alatt van
else {kamu_i++;kamu_b=1;} //csak azért kell, hogy az if és az else ágak végrehajtási ideje nagyából azonos legyen
if (maxjelzo==0 and minjelzo==1) {minjelzo=0;} //még nem volt maximum úgy találtunk minimumot, várunk egy maximum értékre, hogy biztosan a minimum tartományba érkezés
//első pontját találjuk meg. Ez pontosítja a periódusidő mérést
else {kamu_b=0;} //csak azért kell, hogy az if és az else ágak végrehajtási ideje nagyából azonos legyen
if (minjelzo==1 and maxjelzo==1) { //voltunk maximumban, és így a köztes sávon áthaladva lett minimum, ez rögtön az első minimum határ alatti pont
minimum_db++;maxjelzo=0;minjelzo=0; //számolunk egyet, és maxjelzo és minjelzo 0-ra állításával biztosítjuk, hogy erre a sorra csak akkor jövünk
//legközelebb, ha előtte áthaladtunk a maximum értéken. Tehát csak egyetlenegyet számolunk mindaddig amig
//alsó határ alatt van a feszültség
if (start_jelzes==0) {
idotmp=micros();start_jelzes=1;minimum_db=0; //a legeslegelső beszámolt minimum hely megtalálásakor indítjuk az idő mérést, és 0-ra állítjuk a számlálót
//töröljük a periódusidő számítás segéd változóit is
minszam=0; //ebben a változóban számoljuk azoknak a mintavételeknek a számát, amikor a mért feszültség az alsó határ alatti (minimum fesz közelében van
maxszam=0; //ebben a változóban számoljuk azoknak a mintavételeknek a számát, amikor a mért feszültség az felső határ feletti (maximum fesz közelében van
koztesszam=0; //ebben a változóban számoljuk azoknak a mintavételeknek a számát, amikor a mért feszültség az alsó és a felső határ között van (felfutó és lefutó szakasz a minimum és maximumok között)
gyujto=0; //töröljük az effektív feszültség számításához a mintavételek négyzetének tárolóját is
}
}
} while (minimum_db<5); //5 minimumhely megtalálása után kilépünk a ciklusból, az 5 ciklus idejéből fogunk számolni
periodusido=(float) (micros()-idotmp)/minimum_db/1000000; //milisec-re konvertáljuk a mikrosec-ben mért időt, közben 5-el is osztunk, mert 5 ciklust mértünk be
//nem írtam be számmal az 5-öt mert így könnyebb változtatni a a mért ciklusok darabszámát
frekvencia=1/periodusido; //meghatározzuk a frekvenenciát a periódusidőből. A frekvencia változó int, így csak az egész értéket tartjuk meg
koztes_max=koztesszam*(float)maxszam/(minszam+maxszam); //A kitöltési tényező számításához az alsó és a felső határ között eltöltött időszak mintavételeinek számát
//felosztjuk az alsó alatti és a felső feletti mintavételek arányában
kitoltes=(float)(maxszam+koztes_max)/(maxszam+koztesszam+minszam)*100; //a maximum felett eltöltött időszak a "van jel" állapot, erre számoljuk a kitöltési arányt.
//az eredményt rögtön százalékra adjuk meg, a kitoltes változó int, így csak az egész értéket tartjuk meg
min_fesz=feszmin*(float)5/1024;
max_fesz=feszmax*(float)5/1024;
atl_fesz=(max_fesz-min_fesz)/2+min_fesz;
eff_fesz=sqrt(gyujto/(minszam+maxszam+koztesszam))*(float)5/1024;
/*******************Kiírjuk azeredményt************************/
Serial.print("Min:");Serial.print(min_fesz);Serial.print("V Max:");Serial.print(max_fesz);Serial.print("V Atl:");
Serial.print(atl_fesz);Serial.print("V Eff:");Serial.print(eff_fesz);Serial.print("V ");
Serial.print(periodusido*1000,1);Serial.print("msec ");Serial.print(frekvencia,0);
Serial.print("Hz ");Serial.print(kitoltes);Serial.println("% ");
if (idotmp1+1000<millis()) { //egy másodpercenként megismételjük a minimum és maximum keresést, hátha változott
feszmax=0; //töröljük a feszmax értékét, így a loop első do ciklus újra kezdi a maximum tárolását
//amíg ezt nem töröljük a ciklus mindig az előforduló maximumot határozza meg, és ha nem törölnénk
//és a maximum érték csökken, akkor azt nem veszi észre
feszmin=1023; //ugyanaz mint a maximumnál leírt, csak a minimumra
idotmp1=millis();
}
}
Az A0 analóg bemenetet használtam a feszültség mérésére. A négyszögjelet az Arduino D3 kivezetéséről „loptam”, nyilván mindig újra töltöttem a programot, ha más kitöltési tényezőre volt szükség. Ahhoz, hogy egy valódi szinuszjelet is meg tudjak vizsgálni, a jelet egyenirányítani kelett. Ehhez egy 12V-os régi modem tápegységet használtam, ami 12V AC váltó feszültséget állított elő. Mivel az Arduino analóg bemenete nem visel el negatív feszültséget, egyenirányítottam, és egy kicsi feszültség osztás is kellett, hogy a feszültség maximuma kisebb legyen, mint 5V. Így nézet ki ez a komoly mérési segédeszköz:

Ezzel a jelalakkal egy valódi szinusz jelet mértem meg, amilyen egy konnektorban lévő AC230V is lenne. Egy valódi effektív mérő a váltakozó jel esetén a negatív félperiódust hozzáadja a pozitív félperiódushoz, mert (-)feszültség szorozva (-)árammal az pozitív teljesítmény a matematika szabályai szerint. Ezt nálam az egyenirányító végezte el. Kicsi torzulást okoz a jelben a graetz híd, mert a diódák 0,7V-nál nyitnak ki. Azonban ezt most elhanyagoltam, mert a kb. 18V-os feszültség csúcsértéket, a hibával együtt kb. ötödére csökkentettem az ellenállásból készített feszültségosztóval.
Vizsgáltam még szinusz jelalakot, ami csak pozitív feszültséget tartalmazott, azaz olyan oszcillátort használtam, ami offszet beállítási lehetőséget is tartalmazott. A kimenő váltakozó szinuszt el lehetett tolni a pozitív feszültség tartományba. Ugyanez az oszcillátor szerencsére háromszög jelet is elő tudott állítani, így erre a jelalakra is kipróbálhattam az algoritmusom működését. Az oszcillátor egy Aliexpressz-en vásárolt olcsó cucc! Itt találsz leírást a működéséről. Nem egy stabil, kifejezetten gyenge darab, de ez nekem most kapóra jött, mert nem tökéletes jelekkel akartam kipróbálni a működést. Kivéve az Arduino kimenet négyszögjele, mert az szerintem tökéletesnek számított, és nemigen tudtam rontani rajta!
Ahhoz, hogy meg tudjam írni a programot, fontos volt, hogy lással a jelalakot. Ehhez is rendelkezem egy olcsó amatőr oszcilloszkóppal, leírása megtalálható itt! Sajnos ez is egy gyenge darab, bár nekem tökéletesen megfelel. Azonban az oszcilloszkóp beépített mérési lehetőségei és a felbontása inkább csak becslést tettek lehetővé, ezért az általa kijelzett feszültség értékekben nem tudtam megbízni. Pl. az egyenirányított váltakozó feszültség minimumát -0.24V-nak jelezte ki, ami ugyebár biztosan 0V. Ennek ellenére a kijelzett értékek elegendő támpontot adtak arra, hogy az algoritmusom által kiszámolt feszültség értékeknek van-e köze a valósághoz.
Puding prőbája az evés, programomé pedig a mérés!
Egyenirányított szinusz jel
A graetz hidas egyenirányító leosztott kimenő jelét használtam. A következő különböző mérési eredmények születtek. Nem idézem be az összeset, kb. azonos sürüséggel hol ez, hol az lett a végeredmény:
Min:0.00V Max:4.52V Atl:2.26V Eff:3.19V 10.0msec 100Hz 64%
Min:0.00V Max:4.53V Atl:2.27V Eff:3.19V 10.0msec 100Hz 64%
Min:0.00V Max:4.54V Atl:2.27V Eff:3.19V 10.0msec 100Hz 64%
A jelalak képe az oszcilloszkópon:
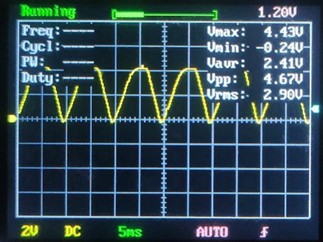
A feszültség maximum változása nem meglepő. Ha a méregdrága mérőműszeremmel rámérek a konnektorra, akkor ott is változik egy kicsit a kijelzett effektívérték. 230V és 235V közötti értékeket szoktam látni. Ha feltételezem, hogy a trafó és az egyenirányító kimenő feszültség maximuma 230V effektív feszültségnél 4,52V, akkor visszafelé számolva a 4.54V 231V feszültséget jelent. Ugyanakkor ezt az ingadozást okozhatta az is, hogy az Arduino referencia feszültsége az 5V tápfeszültség volt, ami a laptopom USB portjának feszültsége. Jelen esetben inkább a hálózati 230V ingadozását valószínűsítem. Ha elhisszük, hogy ennek a szinusz jelnek a feszültség maximuma 4,52V, a táblázatból kiolvasott effektív érték 4.52/1,414=~3,20V. Szinte pont ugyanennyit hozott ki a mintavételezett értékek négyzetének szummájából történt gyökvonás. Ez nagyon meggyőző. Nagyobb pontosságra nincs is szükségem, ez kb. 1%. Már az Arduino is pontatlanabbul mérte a feszültséget, köszönhetően a tápból vett referencia feszültségnek. Mivel 250msec volt az „előmérés”, kb. 2000 mintavételből állapítottam meg a minimum és maximum értéket. Egy félperiódus alatt ez kb. 80 mintavétel lehetett. Következzen egy kis magyarázat, hogy miért 80 mintavétellel számoltam. 12,5 periódust fut be a hálózati 50Hz színuszjele 250msec alatt, ez alatt készült 2000 minta. Tehát egy periódus alatt 2000/12,5=160 mintát vettem, de ezt még felezni kell, mert csak félperiódus áll rendelkezésre. Kíváncsiságból megnéztem egy excel táblában, hogy mennyit változik a szinusz értéke két szomszédos ponton, ha 90 részre osztom fel a 180 fokos tartományt. A 90 az majdnem 80, és ezzel könyebb volt dolgozni, mert a szomszédos értékeket két fokkal kellett változtatni. A szinusz 90fok után és előtt 92 foknál illetve 88 foknál a szinusz értéke 0,9994. Ez még az 5V maximális feszültségnél is csak 5V-(0,9994*5V)=4.997V, amit az Arduino 10 bites ADC pontossága észre sem vesz, így ez engem meggyőzött arról, hogy a maximum értékét megfelelő pontossággal sikerült megállapítani. Ezek alapján az effektív érték, a minimum és maximum és a középérték is megbízható adatnak tűnik, és egy amatőr számára elegendő pontosságú is lehet. A középérték nálam a minimum és a maximum feszültség összegének a fele.
Az, hogy lesz-e, ebből mérőműszer az még mindig nem dőlt el, mert egy mérőműszerhez sok kiegészítő áramkörre lesz szükség, ami még megtervezve sincs, nemhogy hatásukat ismernénk. Nehéz megbecsülni, hogy a műszer elegendően pontos lenne-e az amatőr mérésekhez. Úgy 1-2% pontossággal megelégednék, mert ez azt jelentené, hogy az 5V feszültséget 0.1V pontossággal tudnám megmérni. Ez elegendőnek tűnik számomra. Egy mérés ideje a programmal kb. 250msec+5*20msec (5 periódus) azaz 350msec. Ez három mérés másodpercenként, ez is elegendőnek tűnik.
A kitöltési tényező 64%os értékét még nem értem, ennek pontosan 50%-nak kellene lennie. Ezen még gondolkodnom kell, hogy mi okozhatja. A többi mérésnél reálisnak tűnt, így nem az algoritmus hibájának tartom, valamit nem vettem észre.
Pozitív tartományba tolt 5Hz-es szinusz jel
Ennek a mérésnek a célja főképpen az volt, hogy alacsonyabb frekvencián is megvizsgálja az algoritmus működését. Sajnos az oszcillátorom csak 5Hz-ig tudott lemenni, ez alatt megszűnt oszcillálni, bár a potmétert még bőven lehetett a minimum irányába tekerni. A mérési idő elég hosszú (1,2sec), mert 5 periódus itt már tetemes ideig tart. Ezt azonban el tudom fogadni, ritkán fogok 5Hz-es jelet méregetni.
Az oszcillátor kimenő jele nem túl stabil, kb 50-60mv eltérésekkel szórtak a mért minimumok és maximumok. Ennek megfelelően a számított középérték is ingadozik, de az effektív érték nem változik:
06:32:50.815 -> Min:1.83V Max:4.24V Atl:3.03V Eff:3.09V 204.4msec 5Hz 45%
06:32:52.254 -> Min:1.88V Max:4.25V Atl:3.06V Eff:3.09V 204.5msec 5Hz 44%
06:32:53.660 -> Min:1.82V Max:4.23V Atl:3.02V Eff:3.09V 204.1msec 5Hz 46%
06:32:56.547 -> Min:1.84V Max:4.22V Atl:3.03V Eff:3.09V 204.4msec 5Hz 45%
06:33:00.811 -> Min:1.81V Max:4.23V Atl:3.02V Eff:3.09V 204.3msec 5Hz 46%
Így nézett ki a jel az oszcilloszkópon:
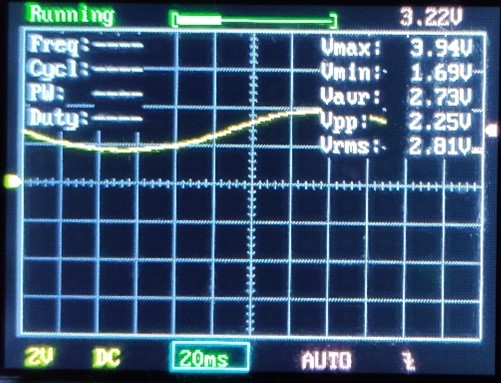
Az effektív érték stabil változatlan értéke amiatt lehet, hogy több ezer mérésből számoltuk ki, és a kicsi egyenetlenségeket elnyomja a statisztika. Az átlag és az effektív érték szinte megegyezik, és ez nem is meglepő. Ebben az esetben ugyanis az effektív érték mérésénél más a helyzet. A szinusz negatív periódusa az offszet feszültséget csökkenti, és minden mért érték pozitív tartományban van. Grafikusan egyszerűbb megmutatni, hogy mi történik:
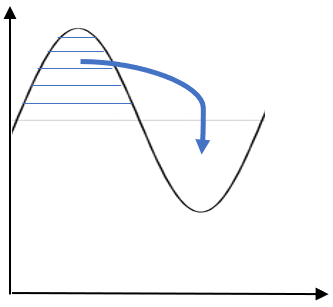
A szinusz felső pupját pont a középértéknél elvágva belemásolhatjuk az alsó bemélyedésbe. Vagyis ez a két félperiódus munkavégzés szempontjából pont kiejti egymást. Ekkor az effektív érték a minimum és maximum érték fele, plusz a minimum érték. Persze ez pont megegyezik a szinusz eltolására szolgáló ofszet feszültséggel, hiszen ezen érték körül változik a jel, de ezt jelen állapotban nem tudom megmérni. Ha esetleg a szinusz jel amplitúdóját minimumra tekertem volna, akkor látható lenne, hol az ofszet feszültség. De most nem látszik, így maradnak a mért értékekből történő következtetések. Tehát a jelen helyzetben várt középérték és effektív érték:
4,22-1,84=2,38/2=1.19+1.84=3,03
A méréssel kimutatott effektív érték majdnem pont ennyi. Sajnos nem tudom megmondani, hogy az eltérést mi okozza, rosszul mérem a minimumot és a maximumot, vagy az oszcilloszkópon nem látható zaj van a mérendő jelen, esetleg az oszcillátor ofszet feszültsége hullámzik egy kicsit?! A nagyságrendek azonban jók, az én elvárásaimnak megfelelnek. Rámértem a jelre a szuper extra mérőműszeremmel is. Elég érdekes értéket mutatott. A feszültség kb 2.7V-ról lassan növekedett 3.3V-ig, majd csökkent majd újra nőtt, úgy 5 másodperces ciklusokban . Nyilván ennyire kicsi frekvencián már nem boldogult a mérendő jellel. Tehát képzeletbeli mérőműszerem már most jobb, mint a méregdrága multiméter!
Pozitív tartományba tolt 50Hz-es szinusz jel
Minden ugyanaz mint előbb, csak a frekvenciát növeltem 50Hz-ra. A mérési idő kb 0.4 sec-re csökkent. Ez nem meglepő, hiszen 250msec minimum maximum meghatározás után 5 ciklust vizsgálok, ami 50hz esetén pont 100msec. Látványosan gyorsult a mérés. Rögtön rámértem a jelre a multiméteremmel, stabilan 3.064V feszültséget mutatott. Ezzel a frekvenciával már boldogult.
Mért értékek:
Min:1.85V Max:4.22V Atl:3.03V Eff:3.09V 20.1msec 50Hz 45%
Min:1.79V Max:4.22V Atl:3.01V Eff:3.09V 20.2msec 50Hz 46%
Min:1.83V Max:4.21V Atl:3.02V Eff:3.09V 20.2msec 50Hz 46%
Min:1.83V Max:4.26V Atl:3.04V Eff:3.09V 20.2msec 50Hz 45%
Min:1.81V Max:4.22V Atl:3.02V Eff:3.10V 20.2msec 50Hz 46%
Min:1.88V Max:4.22V Atl:3.05V Eff:3.09V 20.2msec 50Hz 45%
A minimum és maximum szórása hasonló. Effektív érték áll mint a cövek.
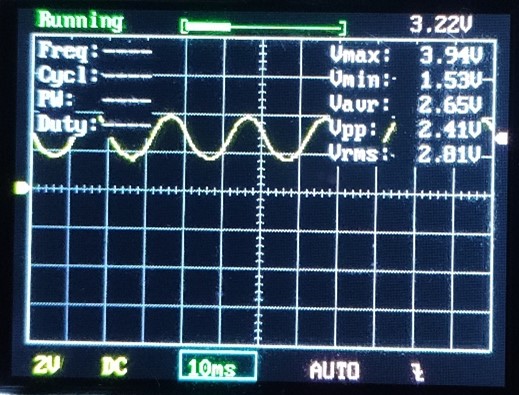
Pozitív tartományba eltolt háromszög:
Ez a mérés ugyanaz mint az előző szinusz jeles mérés, csak háromszög jelalakkal. Nem várható lényeges eltérés, az effektív értéknek ugyanannyinak kell maradnia, hiszen itt is a háromszög felső része belefordítható az alsó részébe (lásd szinusznál lerajzolt magyarázó ábrát), vagyis a középértéket kell megkapnunk.
Mért értékek:
Min:1.62V Max:4.38V Atl:3.00V Eff:3.08V 19.9msec 50Hz 47%
Min:1.63V Max:4.38V Atl:3.00V Eff:3.09V 19.8msec 50Hz 48%
Min:1.59V Max:4.38V Atl:2.99V Eff:3.08V 19.8msec 50Hz 48%
..és ez is történt. Gyakorlatilag alig változott valami. A minimum és a maximum értéke azonban kicsit csökkent. Ez szinte biztos, hogy az oszcillátor hibája. Egy jumpert kellett átdugni, hogy a kimeneten háromszögjel legyen. Tapasztaltam, hogy ilyenkor a feszültség csúcsok kicsit változnak.
A multiméter által mutatott érték is alig változott: 3.059V
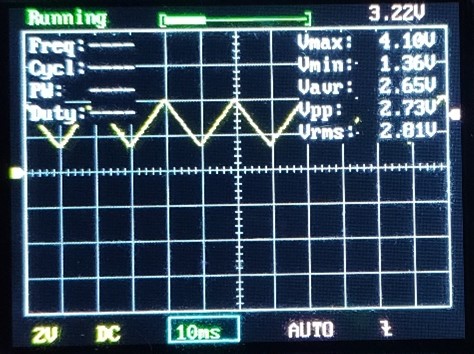
Pozitív tartományba tolt 500Hz-es szinusz jel
Tovább növeltem a frekvenciát, és újra visszakapcsoltam szinusz jelre. Sajnos pont 500Hz-t nem sikerült beállítani. Ez már lehet, hogy az algoritmus hibája, mert nagyon kicsi a periódus idő, én nem biztos, hogy pontos a periódus idő mérése. Ha zajos a jel, akkor minden periódusban eltolódhat a kezdő pont meghatározása. Azért, mint látható, nem tragikus a helyzet, még használhatók az eredmények. …és az is lehet, hogy az oszcillátor ilyen szar!! Erre abból is lehet következtetni, hogy a 5-50Hz tartományban sokkal stabilabb az 50Hz frekvencia, mint az 50-500Hz tartományban. Ezért az 50hz-s mérést az alacsonyabb sávba állítva végeztem. Mérési idő kb 0.3sec, ennél már nem lesz gyorsabb!
Min:1.80V Max:4.32V Atl:3.06V Eff:3.10V 2.0msec 506Hz 45%
Min:1.70V Max:4.32V Atl:3.01V Eff:3.10V 2.0msec 506Hz 47%
Min:1.87V Max:4.40V Atl:3.13V Eff:3.10V 2.0msec 506Hz 41%
Min:1.81V Max:4.40V Atl:3.11V Eff:3.10V 2.0msec 505Hz 43%
Min:1.71V Max:4.40V Atl:3.06V Eff:3.10V 2.0msec 507Hz 46%
Min:1.72V Max:4.26V Atl:2.99V Eff:3.10V 2.0msec 505Hz 47%
Min:1.69V Max:4.22V Atl:2.96V Eff:3.12V 2.0msec 508Hz 48%
A multiméter stabilan 3.074V feszültséget mutatott!
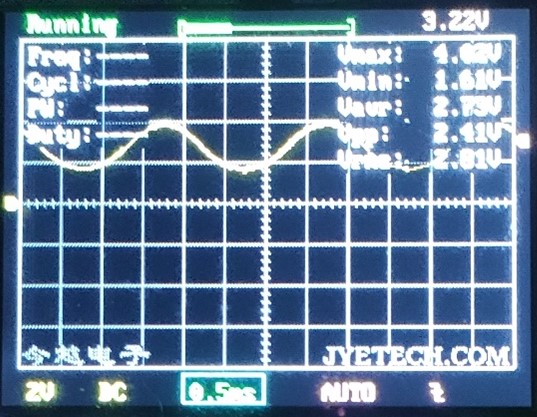
Mínusz tartományba átlógó szinusz:
Itt már az Arduino épségét kockáztattam, mivel elkezdtem negatív tartományba vinni a jelet. Nyilván negatívba nem tud mérni, így azt várom, hogy az effektív érték hamis lesz, azaz a negatív félperiódust nem vonja ki, így növekedik majd az értéke a középértékhez viszonyítva. Nem az történt amit vártam! Nőni kezdett az effektív érték a középértékhez képest, de már akkor, amikor a minimum megközelítette a nullát! Van itt valami, amit nem látok, talán zaj?
Min:0.25V Max:2.70V Atl:1.47V Eff:1.69V 19.9msec 50Hz 48%
Még tovább csökkentve a feszültséget a minimum már rég nulla, a maximum pedig valahol a szinusz félperiudus feszültségén (így állítottam be).
Min:0.00V Max:1.35V Atl:0.67V Eff:0.65V 19.9msec 50Hz 31%
Nem értem, hogy itt mi történt! Az effektív értéknek definició szerint a csúcs / gyök2-nek kellene lennie. Ezen még dolgozni kell!
Négyszögjel:
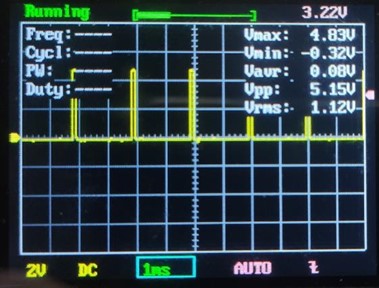
Ez a legizgalmasabb számomra, hiszen jellemzően négyszögjelek fordulnak elő az amatőr gyakorlatomban. Itt nem az effektív érték a lényeges, hanem a periódusidő és a frekvencia, valamint a kitöltési tényező. A méréshez az Arduino D3 kivezetését használtam fel. Közvetlenül összekötöttem az A0 analóg bemenettel. Ezért is kellett használnom a mérés sorozatban a tápfeszt referenciának, és nem a beépített 1.1V-os referencia forrást, ami biztosan pontosabb. A program setup részében elhelyeztem az alábbi két sort:
pinMode(3,OUTPUT);
analogWrite(3,15);
A számított kitöltséi tényező 15/256=0,058 -> 5,8%
Mérési eredmények:
07:41:00.764 -> Min:0.00V Max:5.00V Atl:2.50V Eff:1.21V 2.0msec 489Hz 5%
07:41:01.033 -> Min:0.00V Max:5.00V Atl:2.50V Eff:1.21V 2.0msec 489Hz 5%
07:41:01.302 -> Min:0.00V Max:5.00V Atl:2.50V Eff:1.21V 2.0msec 489Hz 5%
07:41:01.572 -> Min:0.00V Max:5.00V Atl:2.50V Eff:1.21V 2.0msec 489Hz 5%
07:41:01.841 -> Min:0.00V Max:5.00V Atl:2.50V Eff:1.22V 2.0msec 495Hz 5%
07:41:02.079 -> Min:0.00V Max:5.00V Atl:2.50V Eff:1.22V 2.0msec 493Hz 5%
07:41:02.346 -> Min:0.00V Max:5.00V Atl:2.50V Eff:1.21V 2.0msec 488Hz 5%
07:41:02.614 -> Min:0.00V Max:5.00V Atl:2.50V Eff:1.21V 2.0msec 489Hz 5%
07:41:02.883 -> Min:0.00V Max:5.00V Atl:2.50V Eff:1.21V 2.0msec 488Hz 5%
07:41:03.152 -> Min:0.00V Max:5.00V Atl:2.50V Eff:1.21V 2.0msec 489Hz 5%
07:41:03.421 -> Min:0.00V Max:5.00V Atl:2.50V Eff:1.21V 2.1msec 488Hz 5%
07:41:03.657 -> Min:0.00V Max:5.00V Atl:2.50V Eff:1.22V 2.0msec 494Hz 5%
07:41:03.929 -> Min:0.00V Max:5.00V Atl:2.50V Eff:1.21V 2.0msec 489Hz 5%
07:41:04.204 -> Min:0.00V Max:5.00V Atl:2.50V Eff:1.21V 2.0msec 489Hz 5%
Itt most egy teljes mérési sorozatot idéztem, be, hogy látható legyen a gyakoriság. Benthagytam a soros port időkijelzését is.
Láthatóan itt sem pontos a mutatott frekvencia értéke, pedig az Arduino kvarcz órajele miatt a kitöltés és a frekvencia is biztosan pontos. Tehát az algoritmus nem tökéletes, de nem is használhatatlan. Érdemes még ránézni a multiméterre:0.3V-ot mutatott. Itt már azonnal látszik az effektív érték mérésének létjogosultsága. Ha egy ellenállást teszünk a kimenetre, akkor pl 100mW teljesítmény alakul hővé teljes kitöltsénél, akkor a 15/256 kitöltséi tényezőnél 5,8mW lesz az effektív teljesítmény. Kis gondolkodással belátható, hogy ennek a teljesítménynek állandó jelnél pont az 1,21V felel meg. Sem az átlag, sem a multiméter által mutatott érték nem mond semmit a jelről.
A oszcilloszkópon közben ez látható:
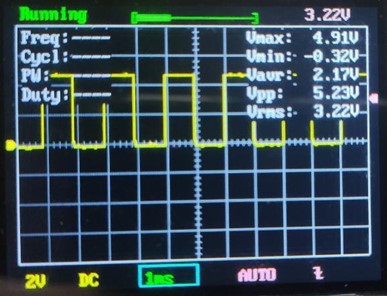
Változtassuk meg a kitöltséi tényzőt 50%-ra. A programban a változás:
pinMode(3,OUTPUT);
analogWrite(3,128);
Eredmények:
07:43:47.957 -> Min:0.00V Max:5.00V Atl:2.50V Eff:3.63V 2.1msec 488Hz 52%
07:43:48.226 -> Min:0.00V Max:5.00V Atl:2.50V Eff:3.62V 2.0msec 494Hz 52%
07:43:48.492 -> Min:0.00V Max:5.00V Atl:2.50V Eff:3.62V 2.0msec 493Hz 52%
07:43:48.763 -> Min:0.00V Max:5.00V Atl:2.50V Eff:3.63V 2.0msec 489Hz 52%
07:43:49.035 -> Min:0.00V Max:5.00V Atl:2.50V Eff:3.55V 2.1msec 488Hz 50%
07:43:49.306 -> Min:0.00V Max:5.00V Atl:2.50V Eff:3.45V 2.0msec 493Hz 47%
07:43:49.540 -> Min:0.00V Max:5.00V Atl:2.50V Eff:3.63V 2.0msec 489Hz 52%
07:43:49.812 -> Min:0.00V Max:5.00V Atl:2.50V Eff:3.63V 2.1msec 488Hz 52%
07:43:50.082 -> Min:0.00V Max:5.00V Atl:2.50V Eff:3.57V 2.0msec 494Hz 51%
07:43:50.353 -> Min:0.00V Max:5.00V Atl:2.50V Eff:3.63V 2.0msec 490Hz 52%
07:43:50.621 -> Min:0.00V Max:5.00V Atl:2.50V Eff:3.55V 2.1msec 488Hz 50%
07:43:50.858 -> Min:0.00V Max:5.00V Atl:2.50V Eff:3.63V 2.0msec 488Hz 52%
07:43:51.128 -> Min:0.00V Max:5.00V Atl:2.50V Eff:3.63V 2.1msec 488Hz 52%
07:43:51.399 -> Min:0.00V Max:5.00V Atl:2.50V Eff:3.63V 2.0msec 488Hz 52%
07:43:51.669 -> Min:0.00V Max:5.00V Atl:2.50V Eff:3.63V 2.1msec 488Hz 52%
Meglepő lehet, hogy az effektív érték nem az 5V feszültség felének adódik. Ismét ne felejtsük el, hogy négyezetes mennyiségről van szó. A multiméter még mindig marhaságokat mutat: 0.6V!! Az oszcilloszópon meg ezt láttam:
Tovább növeljük a kitöltséi tényezőt.
pinMode(3,OUTPUT);
analogWrite(3,240);
A számított kitöltséi tényező 241/256=0,941 ->94,1%
Mérési eredmények:
07:45:31.361 -> Min:0.00V Max:5.00V Atl:2.50V Eff:4.84V 2.0msec 494Hz 94%
07:45:31.629 -> Min:0.00V Max:5.00V Atl:2.50V Eff:4.85V 2.0msec 488Hz 94%
07:45:31.901 -> Min:0.00V Max:5.00V Atl:2.50V Eff:4.85V 2.0msec 488Hz 94%
07:45:32.135 -> Min:0.00V Max:5.00V Atl:2.50V Eff:4.85V 2.0msec 490Hz 94%
07:45:32.402 -> Min:0.00V Max:5.00V Atl:2.50V Eff:4.85V 2.0msec 489Hz 94%
07:45:32.673 -> Min:0.00V Max:5.00V Atl:2.50V Eff:4.85V 2.0msec 488Hz 94%
07:45:32.942 -> Min:0.00V Max:5.00V Atl:2.50V Eff:4.85V 2.0msec 488Hz 94%
07:45:33.210 -> Min:0.00V Max:5.00V Atl:2.50V Eff:4.85V 2.0msec 488Hz 94%
07:45:33.482 -> Min:0.00V Max:5.00V Atl:2.50V Eff:4.85V 2.0msec 488Hz 94%
07:45:33.718 -> Min:0.00V Max:5.00V Atl:2.50V Eff:4.85V 2.0msec 490Hz 94%
07:45:33.989 -> Min:0.00V Max:5.00V Atl:2.50V Eff:4.84V 2.0msec 494Hz 94%
07:45:34.263 -> Min:0.00V Max:5.00V Atl:2.50V Eff:4.84V 2.0msec 494Hz 94%
07:45:34.530 -> Min:0.00V Max:5.00V Atl:2.50V Eff:4.84V 2.0msec 494Hz 94%
07:45:34.802 -> Min:0.00V Max:5.00V Atl:2.50V Eff:4.84V 2.0msec 494Hz 94%
07:45:35.041 -> Min:0.00V Max:5.00V Atl:2.50V Eff:4.85V 2.0msec 490Hz 94%
Az értékek magukért beszélnek. Frekvencia sajnos kicsit változik, de ez mérési hiba. A kitöltséi tényező viszont egész jó. A multiméter még mindig nem tudja hol jár: 1.47V.
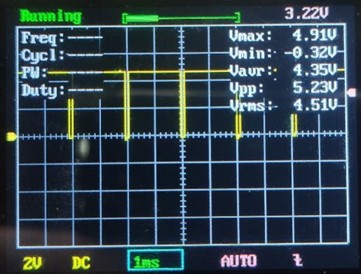
Tanulság, hogy van még mit faragni az algoritmuson. Már próbálkoztam optimalizálással, az algoritmusban az if vizsgálatokhoz csináltam else ágat, és kamu utasításokkal töltöttem fel, hogy a végrehajtási idő azonos legyen a feltétel igaz és hamis esetén is. Ez már benne van a közölt program forrásban. Ennyi még nem volt elég! Azonban az eredmény számomra kielégítő, nekikezdtem a műszer további részeinek tervezésébe.
