Tartalom:
- Abszolut alapok teljesen kezdőknek
- Feszültség, áramerősség, ellenállás, kondenzátor
- Ellenállások soros és párhuzamos kapcsolása, eredő számítása
- Váltakozó áram, egyenirányító, szűrő
- Tekercs, transzformátor
- Tranzisztor, MOSFET
————————————————————-
Ebben a fejezetben igyekeztem összefoglalni azokat az alapismereteket, melyek feltétlenül szükségesek egy kezdő elektronikai amatőr számára. Tudnod kell, hogy mindent jelentősen leegyszerűsítek annak érdekében, hogy könnyebben érthető legyen. Tudományos értelemben nem vagyok “szakszerű”, de a megértéshez ez is elég. Ha pontosabb infókat szeretnél, akkor keresd fel a Wikipédiát, vagy pl. a Digitális tankönyvtárat. Találsz leírásokat a hobbielektronika.hu és a tavir.hu weboldalakon is.
Segítség lehet a leírtak megértésében egy áramkör szimulátor program. Jómagam is csak mostanában ismertem meg a működését, és néhány mintapéldát virtuálisan is megvalósítottam. Nagyon megtetszett! Javaslom, hogy töltsd le megadnak ezt a szimulátor programot, és használd. A mintapéldákat le lehet a weblapomról menteni és betölteni a szimulátorba. Itt találod a szimulátor telepítéséről és használatáról szóló leírásomat, valamint a mintapéldák is megtalálhatók ugyanitt az ismertető szövegében elhelyezett hivatkozásokban.
Feszültség:
A körülöttünk található fémek (vas,réz, arany) egyik tulajdonsága, hogy a bennük lévő elektronnak nevezett részecskék elmozdulhatnak, és összevissza vándorolhatnak a fémen belül. Időnként az is előfordul, hogy valamilyen külső körülmény hatására egy bizonyos helyen több lesz belőlük, mint máshol. Annak jellemzésére használjuk a feszültséget, hogy milyen nagy az elektron többlet az egyik pontban egy másik ponthoz képest. A feszültség mértékegysége a “volt” és V betűvel szoktuk jelölni. Pl. a ceruza elem 1,5V-os feszültséget szolgáltat. Ha nagyobb feszültségre van szükséged, akkor több elemet kell sorba kapcsolni. Pl. ha három elemet egymáshoz kapcsolsz a képen látható módon, akkor 4,5V feszültséget kapsz:
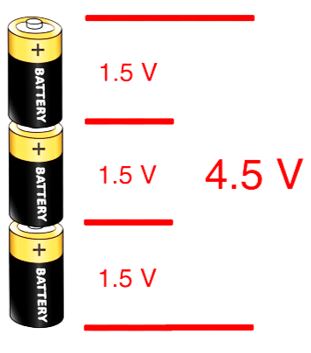
Ha elemeket használunk, akkor tudnunk kell, hogy ez egyenáramú áramforrás. Vagyis van egy pozitív és egy negatív kivezetése. Ezeket nem szabad összekeverni.
Az Arduino eszközök 5V feszültséget használnak. Elemekből nem lehet pont 5V-ot összerakni, de léteznek olyan elektronikus áramkörök, melyekkel nagyobb feszültségből tetszőleges kisebbet lehet csinálni.
Egy Nikola Tesla nevű tudós munkájának köszönhetően nem csak elemekkel táplálhatjuk elektromos eszközeinket. Az erőművekben gőzzel és más motorokkal hajtott forgó generátorok termelnek nekünk váltakozó feszültséget. A konnektorunkban kb. 230V feszültség található, ami másodpercenként 50-szer változtatja meg a polaritását, azaz felcserélődik a pozitív és a negatív kivezetés, ami a generátor forgó mozgásával van összefüggésben. Ebből a váltakozó feszültségből a telefontöltőnk 5V feszültséget csinál, méghozzá egyenfeszültséget. Ez nagy szerencse, mert az elemek nagyon drágák!
Áram:
Ha egy feszültségforrás pozitív és negatív pontját összekötjük egy drótdarabbal, akkor azok a bizonyos elektronok a fémben szabadon mozogva elindulnak az elektron többlettel rendelkező helyről az elektron hiányos területre. Ezt hívjuk elektromos áramnak (mert az elektronok „áramlanak”). Miközben mozognak, ütköznek a fémdrót atomjaival, amik ettől felmelegszenek, mozgásukkal mágneses teret is keltenek. Tehát az elektronok áramlása munkát végez. Minél nagyobb a feszültség (nagyobb elektron többlet az egyik helyen), annál nagyobb áram folyhat a vezetékben. Hogy mekkora ez az áram, az a vezeték méretétől is függ. Ha a vezeték vastag, akkor sok elektron mozoghat egyszerre. Tehát az áram nagysága nem csak a feszültségtől függ, hanem valami mástól is.
Ellenállás:
Ez a valami az ellenállás. Az ellenállás az áramot vezető drótdarab tulajdonsága. Minél vastagabb egy drót, annál kisebb, minél hosszabb a drót, annál nagyobb az ellenállása.
A drót anyagától is függ a vezetőképessége. Egy aranyból készült drót, nagyon jól vezeti az áramot, tehát kicsi az ellenállása. Jól vezeti még az áramot a réz. Kevésbé jól az alumínium. Ha a drót anyaga nem tiszta fém, akkor olyan nagy is lehet az ellenállás, hogy az izzólámpánk amit a vezetékkel a konnektorba dugunk, nem is fog világítani. Ezért készülnek a villanyvezetékek általában rézből. Egyes anyagok, mint pl. a gumi, pvc, üveg egyáltalán nem vezetik az áramot, vagyis nagyon nagy az ellenállásuk. Ezeket szigetelő anyagoknak hívjuk.
Van amikor a vezeték ellenállásának a növelése kifejezetten fontos, mert csökkentenünk kell az áram nagyságát, hogy egy alkatrész ne menjen tönkre. Pl. a LED világításokban korlátozni kell a LED-en átfolyó áramot. Olyan nagy ellenállás kell, hogy azt fém huzallal már nem is lehet gazdaságosan előállítani, ezért találták ki az ellenállásnak nevezett elektronikai alkatrészt.
Ohm törvénye:
Már nem ússzuk meg, hogy egy kis matematikát is vigyünk a dologba. Georg Simon Ohm (1789-1859) német fizikus vizsgálta a vezetőképesség, áram és feszültség matematikai kapcsolatát. Így néz ki a róla elnevezett összefüggés:
R = U / I
Ebben a képletben az R az ellenállás, U a feszültség, I az áram. Nem bonyolult! Szavakkal annyit jelent, hogy a vezeték ellenállása kiszámolható a feszültség és az átfolyó áram hányadosaként.
Nézzünk rá példát. Ha a telefonunk 5V (Volt) feszültségről töltődik és éppen 1A (amper) áramot fogyaszt, akkor az ellenállása 5V/1A=5 ohm. Ez most még nem sokat jelent számunkra, de ki lehetett számolni az ellenállást. Az ellenállás mértékegysége az ohm (Ω). Az elektronikában nagyon-nagyon kicsi áramokat használunk. Főleg ha elemekkel vagy kisméretű akkumulátorokkal tápláljuk az áramkörünket. Az amper ezred része körüli áramok már nagyon nagynak számítanak. Pl. egy LED zseblámpánkban levő világító alkatrész kb. 0,02A (20mA) áramot fogyaszt. A TV kikapcsolt állapotában világító piros kis fény előállításához már 1mA is elég.
Érdemes tudni, hogy egy átlagos ceruzaelem, 10mA (milliamper, az amper ezred része) áramot szolgáltatva 4-5 nap alatt lemerül. Számoljuk is ki, hogy mekkora egy 10 mA fogyasztású áramkör eredő ellenállása:
5V / 0,01A = 500 Ω
Tehát áramköreinkben a több száz Ω-os vagy még ennél is sokkal nagyobb ellenállásokkal fogunk leggyakrabban találkozni. A nagyobb értékű ellenállásokat ezért nem is Ω-ban, hanem KΩ (kiloohm, az ohm ezerszerese) vagy MΩ (megaohm, az ohm egymilliószorosa) értékben szokták megadni. A leírásokban az Ω jelet nem mindíg használják, helyette kiírják, hogy “ohm”, mert ez így egyszerűbb. Én is így fogok tenni, hol kiírom az “ohm”-ot, hol használom a Ω jelet, ahogy éppen eszembe jut.
Ellenállások eredője, áramok és feszültségek:
Ha van egy ellenállásunk és azt rákötjük pl. egy telefontöltő két kivezetésére, akkor áramkört kapunk. Azért áramkör, mert a telefontöltő egyik kivezetéséből indulva az ellenálláson keresztül körben haladva elérünk újra a telefontöltőhöz. Az ellenálláson keresztül nyilván áram fog folyni. Ezt az elrendezést jelentősen leegyszerűsítve szoktuk lerajzolni, és ezt hívjuk áramköri kapcsolási rajznak (röviden: kapcs. rajz):
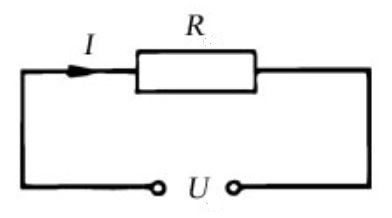
Ebben minden benne van ami nekünk kell. A telefontöltőnket két pöttyel szimbolizáltuk az “U” betű két oldalán. Az “U” a feszültség jele. Az áramkörben folyó áramot egy pici nyilacska jelzi, ezt már később nem fogjuk berajzolni, de most mutatja, hogy merre folyik az áram. Az áram betűjele az “I”. Az ellenállás szimbóluma hasonlít arra, ahogyan egy valós ellenállásnak nevezett alkatrész kinéz:

Annyira kicsik szoktak lenni ezek az alkatrészek, hogy az ellenállás értéket színes csíkokkal szokták ráfesteni, mert számok nem férnek rá. A neten lehet ellenállás érték színjelölés táblázatot találni, ennek segítségével megfejthető az ellenállás érték. Másik lehetőség, hogy megmérjük ellenállás mérővel.
Az ellenállás betűjele R. Ha bármiből több is van az áramkörben, akkor a betűjel mögé írt kicsike számmal (index) szoktuk megkülönböztetni az egyes alkatrészeket. Tételezzük fel, hogy áramkörünkben az U feszültséget egy 5V-os telefontöltő szolgáltatja. Elektronikai alkatrész dobozunkból egy 1 KΩ-os ellenállást sikerült előkapnunk. Mekkora áram folyik az áramkörben? Ehhez rendezzük át az Ohm törvény képletét:
R = U / I ==>> I = U / R
A második egyenletből már könnyű dolgunk van: I = 5V / 1000 Ω = 0,005A. Az ennyire kicsi áramokat inkább milliamper-ben szoktuk megadni, vagyis 5mA áram folyik az áramkörben. Sok ez vagy kevés? Egy telefontöltő általában 1A áramot tud szolgáltatni (1000 mA), tehát ehhez képest nagyon kevés. Ha elemről táplálnánk áramkörünket, akkor egy hónapig sem működne, ebben az esetben meg sok.
Ha van két ellenállásunk, azt sorba köthetjük, és úgy kapcsolunk rá feszültséget. Ezt hívjuk soros kapcsolásnak:
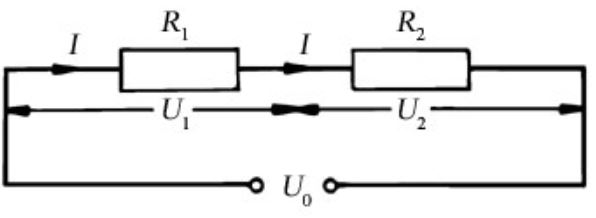
Az áram csak egy úton haladhat körbe ebben a kapcsolásban, ezért mindkét ellenálláson ugyanakkora az átfolyó áram. Mivel az ellenállások értéke így összeadódik az eredő ellenállás
Re=R1+R2.
A U0 tápfeszültség legyen most egy telefontöltő 5V-os feszültsége, amit a két bemeneti pontra kapcsolunk. Legyen az R1 és R2-vel jelzett ellenállásunk értéke 1-1 Kohm. Máris tudhatjuk, hogy az áramkörben folyó áram 5V/2Kohm=2,5mA. nyilak közé írt U1 és U2 betűk az ellenállásokon eső feszültséget jelentik. Jelen esetben ezek a feszültségek azonosak mert azonos értékűek az ellenállások. Vagyis U1 és U2 is egyaránt 2,5V. Ezt ki is számolhattuk volna, nem csak megsejtjük. Ohm törvénye alapján ez is egyszerű. Rendezzük át Ohm törvény képletét a feszültségre:
R = U / I ==>> U = R * I
Tudjuk, hogy az áram 2,5 mA, az ellenállás értéke pedig 1 KΩ.
1000 Ω * 0,0025 =2,5V.
Fontos, hogy az ellenállás értékét mindig Ω-ban, a feszültséget V-ban, az áramot pedig A-ben adjuk meg.
Most változtassunk az áramkörünkön, és legyen az R1=500Ω az R2=1,5KΩ.
- Az áramkörben folyó áram 5 V / 2 Kohm = 2,5 mA. (ez nem változott)
- Az U1 (500Ω ellenállás feszültsége) 500Ω*0,0025 A = 1,25 V.
- Az U2 (1,5 KΩ ellenállás feszültsége) 1500 Ω * 0,0025 A = 3,75 V.
Megállapíthatjuk, hogy a sorba kötött ellenállások feszültség osztást végeznek, felosztják a tápfeszültséget az ellenállások értékének arányában.
Játszhatsz az ellenállások soros kapcsolásával egy szimulátor programban is. Itt megismerheted, hogyan kell használni a szimulátort, itt pedig a soros ellenállásokat ismertető kapcsolásról tudhatsz meg többet
Az ellenállásokat azonban nem csak sorba, hanem párhuzamosan is köthetjük:
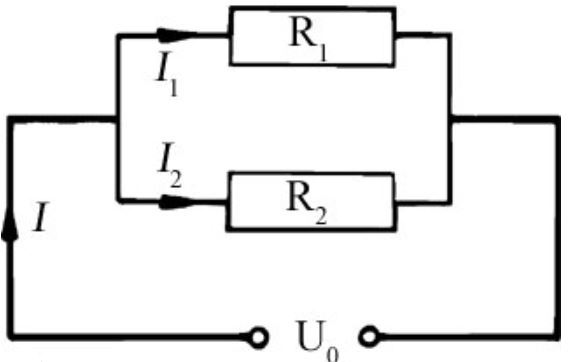
Az ellenállásokra ugyanakkora feszültség kapcsolódik. Most nem az áram azonos, hanem a feszültség. Ennek következtében mindkét ellenálláson I=U/R áram folyik. Az áramok összeadódnak, így a feszültségforrást terhelő áram a két áram összege (I=I1+I2). Az eredő ellenállás (Re) kiszámolása kicsit nehezebb. Re=U/(I1+I2).
Lássunk egy számolást erre az áramkörre is. U legyen most is 5V, R1=1Kohm, R2=2Kohm.
- I1 = 5 V / 1 KΩ = 5 mA
- I2 = 5 V / 2 KΩ = 2,5 mA
- Re= 5V / (5 mA + 2,5 mA) = 0,666 KΩ
Az előbb felhívtam a figyelmet arra, hogy a képletekbe Ω-ot ampert és volt-ot helyettesítsünk be. Ha valaki sokat számolgat, akkor hozzászokik, hogy KΩ megadásakor mA lesz a végeredmény, ezért most bemutató jelleggel felrúgtam a saját szabályomat.
Szimulátorban így néznek ki a párhuzamos ellenállások
Kirchoff törvények:
Meg kell még említeni két igen fontos összefüggést. Annyira triviálisak, hogy nem is igazán szoktunk gondolkodni a dolgon. A névadó Gustav Robert Kirchoff (1824-1884) német fizikus.
Csomóponti törvény: egy csomópontba befolyó és onnan kifolyó áramok összege 0 (zéró). Ha ezt le akarjuk rajzolni, akkor így néz ki (Wikipédia kép):
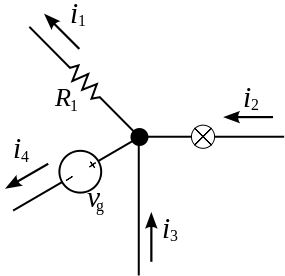
A dologban semmi meglepő nincs. Az áramot úgy kell elképzelni, mintja csővezetékben vizet áramoltatnánk. Ha sok cső találkozásában az egyik csövön valami befolyik, akkor az valahol ki is fog folyni.
Hurok törvény: Egy hurokban a feszültségforrások összege megegyezik a feszültség esések összegével. Lerajzolva:
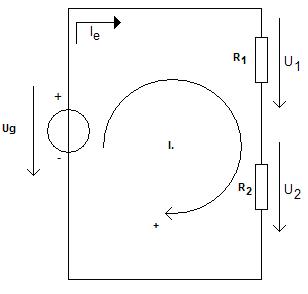
Ez a kép is a Wikipédiából származik. Ha egy áramkörben körbe járunk, akkor előjelesen összegezve a feszültségeket, pont nullát kapunk. Nincs ebben semmi meglepő. Felhívom a figyelmet a feszültségforrás és az ellenállások mellé rajzolt nyilak irányára. Ezek ebben az ábrában mindíg a pozitív pólustól a negatív felé mutatnak. Ha elindulunk a körbe mutató nyíl irányába a feszültségforrás (pl. egy elem) negatív pólusából, akkor szembe mutat a feszültség forrás mellé rajzolt nyíl. Ha elérkezünk az ellenállásokhoz, ott már a körbejárás irányába mutatnak az ellenállások mellé rajzolt nyilak. Előjelesen összeadva valóban nulla a végeredmény. Gondoljunk az ellenállások soros kapcsolásánál végzett számításokra:
5V-1,25V-3,75V=0V
A Kirchoff törvények annyira triviálisak, hagy soha nem is gondolunk rájuk, csak használjuk. Ha sorosan kapcsoljuk az ellenállásokat és egyéb tetszőleges elektronikus alkatrészeket egy áramkörben, akkor a hurok-törvényt használjuk, ha a párhuzamosan kapcsolunk ellenállásokat, akkor a csomóponti-törvényt.
Váltakozó áram és feszültség:
Eddig egyenáramokról beszéltünk. Elemek és akkumulátorok egyenáramot szolgáltatnak. Vagyis ráírták ezekre, hogy melyik a pozitív, és melyik a negatív kivezetés. Jelölni is szokták a feszültség típusát egy “DC” (direct current) felirattal. Azonban az elektronikában nem csak egyenáramokkal találkozunk. Ha egy feszültségforrás pólusai periódikusan felcserélődnek, akkor váltakozó feszültségről (áramról) beszélünk. Ez van a konnektorunkban. A váltakozó feszültség jelölése “AC” (alternating current). Mint látható az AC rövidítésben áramról beszélünk, és nem feszültségről. Mindkét megnevezés helyes, hiszen az áram iránya is változik, nem csak a feszültség polaritása. Váltakozó áram esetén sokkal könnyebb a feszültség szinteket átalakítani, egy transzformátornak nevezett berendezéssel. Ezért az iparban és a háztartásokban is váltakozó áramot használunk. Talán nem mindenki tudja, hogy kezdetben egyenáramú elektromos rendszerek kezdtek elterjedni. Ez a közismert Thomas Alva Edison üzleti vállalkozása volt. A váltakozó áram elterjedését egy George Westinghouse nevű versenytársa szerette volna elérni. Párharcukból a váltóáram került ki győztesként. Egy máig használatos eszköz emlékeztet üzleti harcukra, a villamosszék! Ez Edison reklámfogása volt, amivel a váltóáram veszélyességét szerette volna elhitetni az emberekkel. A váltakozó áramról, és érintésvédelmi tudnivalókról itt tudhatsz meg többet!
A váltakozó áram azonban nem csak a konnektorból jön kifelé. Váltakozó áramot használunk nagyon sok berendezésben pl. a rádió összeköttetést létrehozó berendezésekben is. Ezeknél a berendezéseknél már inkábba váltakozó feszültség elnevezést használnám, mert nem az áram a lényeges, mint a háztartási eszközöknél. Az említett berendezésekben olyan áramkörök működnek, melyeket oszcillátorokak nevezünk. Az oszcillátorok váltakozó feszültséget állítanak elő, méghozzá igen sokféle frekvenciával. A frekvencia azt adja meg, hegy hányszor változik meg a feszültség (áram) iránya egy másodperc alatt.
Az Arduino eszközökben is van oszcillátor, mivel a mikrovezérlőnek órajelre van szüksége. Ez az oszcillátor 16 millió jelet (16Mhz) ad ki magából másodpercenként. Ez az oszcillátor azonban nem váltakozó feszültséget állít elő. A feszültség iránya nem változik meg, csak a feszültség nagysága változik nagyjából 0V és 5V között. Valódi váltakozó feszültséget amatőr gyakorlatban szinte csak a konnektorban fogunk találni.
Váltakozó áram egyenirányítása, a dióda:
Az ellenállás nagyon egyszerű működésű. Nem számít neki, hogy az áram merre folyik, egyszerűen csak ellenáll az áramnak, bármerre folyik is. Ha konnektorunkban váltakozó feszültség van, akkor abból valahogyan egyenfeszültséget kell csinálni, hogy tölthessük a telefonunkat, vagy feszültséggel lássuk el az Arduino áramköreinket. Ehhez kell egy diódának nevezett alkatrész. A részletes fizikai működése kevésbé fontos, ezért azt vizsgáljuk meg, hogyan lesz segítségével váltakozó feszültségből egyenfeszültség. A dióda áramköri jele:

Az áramköri szimbólum meglehetősen beszédes. Az áram akkor folyik át rajta, ha az anód pozitívabb feszültségre kerül, mint a katódja. ekkor a szimbólumban felismerhető nyil arra utal, hogy áram indul meg a pozitív kivezetéstől a negatív felé. Ezt hívjuk nyitó iránynak, mert a dióda úgy csinál mintha egy sima egyszerű vezetékdarab lenne. Ha a pozitív pólust a katódra kapcsoljuk, akkor az áram “falba ütközik”, a dióda lezár, azaz nem folyik rajta áram. Ezt hívjuk záró iránynak. A dióda ekkor úgy viselkedik, mintha elvágtuk volna a vezetéket. Természetesen a valóságos diódák nem ennyire ideálisak. Nyitó irányban jól mérhető, de kis értékű ellenállásuk van, míg záró irányban sem szakadást mutatnak, van ellenállásuk, bár nagyon nagy. Hogyan lehet ezzel egyenirányítani? Hát így:
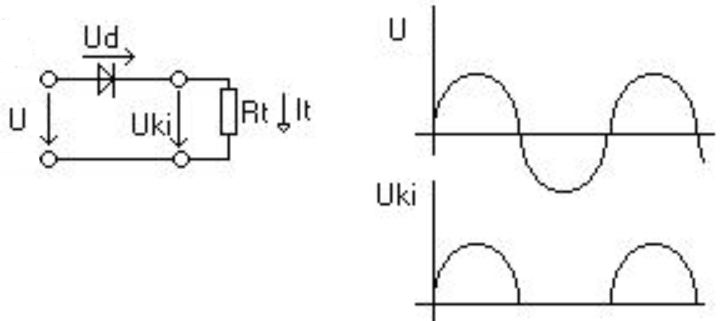
Képzeljük el, hogy a fenti áramkör bemenő feszültsége folyamatosan váltakozik. A jobb oldalon felül egy rajz mutatja az a feszültség időbeli változását. Váltakozva hol pozitív, hol negatív a bemenet egyik pontja a másikhoz képest. Pont ilyen az időbeli változása a konnektorban lévő feszültségnek is. A diódán persze csak akkor folyik át áram, ha az anódja pozitívabb. Ekkor az áram a vele sorba kapcsolt ellenálláson is átfolyik. Az ellenálláson tehát ilyenkor az Ohm törvény alapján U=R*I feszültséget mérhetünk. Ne feledjük, az U feszültség folyamatosan változik, nem csak az iránya a nagysága is. Az álltalános iskolából ismert szinusz függvénnyel egyezik meg a változása. Ezt a szinusz jelet látjuk a jobb felső ábrán. Ha a tápegység feszültsége megfordul, és a dióda záró irányba kerül, akkor nem folyik rajta át áram, tehát az ellenálláson 0V feszültséget mérhetünk. Az ellenálláson eső Uki feszültség időbeni változását a jobb oldalon alul láthatjuk. A dióda láthatóan levágta a bemenő feszültség negatív szakaszát.
A kapcsolás működését érdemes a szimulátorban is kipróbálni itt!
Ezzel kész az egyenáram. Van vele probléma, mert mert nem pont olyan, mint amit az elem szolgáltat. Az elem ugyanis állandó feszültséget ad, ez meg hol van, hol nincs. Ezen majd a következő alkatrész, a kondenzátor fog segíteni. A valóságban így néz ki egy átlagos dióda:

A csíkkal megfestett vége a katód! Ez éppen egy 1N4148 típusú dióda, amin nyitó irányban maximum 150mA áram folyhat át. Záró irányban pedig maximum 75V feszültséget lehet rákapcsolni. Ha ezeket a határértékeket átlépjük, a dióda tönkremegy. A 230V-os hálózatban ezt a diódát ne használjuk. Illetve ne kössünk vele sorba olyan kicsi értékű ellenállást, aminek hatásása az áram nagyobb lesz mint 150mA. 5V feszültség esetén ez kb 33ohm-nál kisebb ellenállást jelent.
Meg kell még említeni hogy nyitó irányban egy diódának nem csak ellenállása van, sajnos kb. 0,7V feszültség is esik rajta. Ez egyben az a feszültség érték, ami alatt a dióda még nem vezeti az áramot. Elmésen nyitó feszültségnek nevezik. Tehát ha egy diódát rakunk egy áramkörbe, akkor számítsunk rá, hogy a dióda után már kisebb lesz a feszültség. Ez általában nem nagy baj, de kisfeszültségű áramkörökben nagy nehézséget okozhat. pl. AC 0,5V feszültséget nem lehet egyenirányítani, mert a soros ellenálláson soha nem fog áram folyni. A gyakorlatban ez azt jelenti, ha van egy 5V feszültségű transzformátorunk, akkor a nyitó feszültség miatt egyenirányítás után már csak 4,3V feszültséget fogunk mérni a soros ellenálláson. Ez van. ezzel együtt kell élnünk.
LED dióda:
Ha már a diódánál tartunk, itt érdemes megemlíteni, hogy van a diódáknak egy speciális típusa a világító dióda (Light Emission Dioda azaz rövidítva LED). Nagyon szeretjük, mert amikor épp nyitó irányban van, akkor fényt bocsát ki. Itt egy fotó, bár ki ne ismerné:

A LED-ek hosszabbik lába az anód, tehát ha azt akarjuk, hogy világítson, akkor a rövidebb láb legyen a negatív, a hosszabbik pedig a pozitív pólusra kötve. A diódák nyitó feszültsége kicsit nagyobb a megszokott 0,7V dióda nyitófeszültségnél. Kb 2-3V közötti érték típustól és sokszor a világítás színétől függően. Ez most éppen egy L-813 GD típusú világító dióda. Ennek nyitó feszültsége 2V. Maximális fényerővel 20mA áramnál világít, ennél nagyobb áram hatására rövid időn belül tönkremegy. Tehát a LED-ek áramát korlátozni kell. Ezt soros ellenállással tehetjük meg:
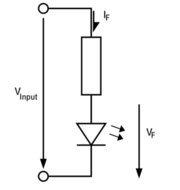
Tételezzük fel, hogy 5V-os telefontöltőre akarjuk kötni a LED-et. Mekkora legyen a soros áram korlátozó ellenállás értéke? Ohm törvény segít. Tudjuk, hogy a LED nyitó feszültsége 2V. Vagyis a soros ellenálláson 3V feszültségnek kell esnie, miközben rajta és a LED-en keresztül 20mA áramnak kell átfolynia. Ebből már tudunk számolni:
R=U/I ==>> R=3V / 0,02A = 150Ω
Tehát ha kb 150-200Ω körüli ellenállást teszünk sorba a LED-el, akkor tökéletesen fog működni. Pont 200Ω-os ellenállást lehet, hogy nem kapunk a boltban, mert az olcsón kapható értékek között 220Ω lesz a legközelebbi. Ez megfelelő lesz. Kicsit kisebb lesz a fényerő, de alig lehet ezt észrevenni. Ha azonban biztosan a maximumot akarjuk kihozni, és nem kapunk 150Ω értéket, akkor két ellenállást kapcsoljunk sorba, egy 100Ω, és egy 47Ω értékűt. Ezek olcsón kaphatóak 3-5Ft/db körüli áron. A fentihez hasonló LED ára 5-10Ft/db. Léteznek teljesítmény LED-ek, amikkel már meg lehet világítani a lakást. Ezek árama akár 2-3A is lehet. Az áruk meg többszáz forint.
Zéner dióda:
Létezik még egy érdekes típusa a diódáknak, ez a Zéner dióda. Áramköri jele és legegyszerűbb bekötése egy áramkörbe:
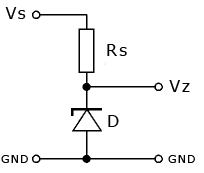
Az a furcsa tulajdonsága van, hogy záró irányban egy meghatározott feszültség értéken mégiscsak kinyit! Mint látható pont fordítva helyeztük el az alkatrészeket, mint az egyenirányító kapcsolásnál. A zéner diódát záró irányba kell bekötni, és egy pontosan meghatározott feszültségen fog áramot vezetni. Így a rajta eső feszültség stabil, állandó érték lesz. Ezzel a kapcsolással és a Zéner típusának megválasztásával különböző kimenő feszültségű tápegységeket lehet készíteni. Ritkán használnak már ilyet, mert nem jó a stabilitása, de gondoltam megemlítem!
Kondenzátor:
Az áramkörökben használt jele kifejezi azt, ahogyan kinéz és amit csinál:
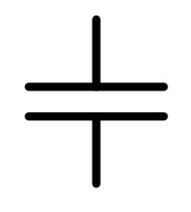
A kondenzátor nem más mint két szemben álló nagy felületű fémlemez, amit szigetelő anyag választ el egymástól. Egy valós kondenzátor így néz ki:

Ha egyenáramot kapcsolunk egy kondenzátorra, akkor nem vezeti az áramot. Azonban a nagy fémfelületen sok-sok elektron foglalhat helyet, vagyis a kondenzátornak töltés tároló képessége van. Ha rákapcsolunk egy elemet, akkor az elemből elektronok áramlanak át az egyik fémlemezre. Ha eltávolítjuk az elemet, az elektronok ottmaradnak, és máris van a kondenzátor két kivezetése között feszültség különbség. Persze pont ugyanakkora, mit az elem feszültsége. Ha most egy fém vezetékkel összekötjük a kondenzátor két kivezetését (rövidre zárjuk), akkor megindul az elektronok áramlása, és addig tart, amíg el nem fogynak az elektronok az elektron többlettel rendelkező helyről. Olyan, mint egy elem, ami gyorsan lemerül.
Kombináljuk össze az egyenirányító kapcsolásunkkal:
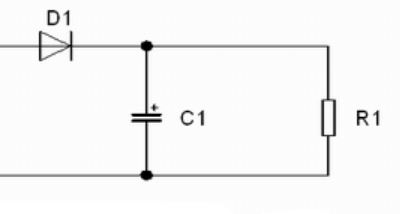
Annyi változás történt, hogy a diódát követő ellenállással párhuzamosan kapcsoltunk egy kondenzátort. Amikor a dióda vezet, elektronok áramlanak a kondenzátorba (és persze az ellenálláson is folyik áram). Amikor a dióda előtt megváltozik a feszültség iránya, és a dióda lezár, magára hagyja a kondenzátort és az ellenállást. A kondenzátorban felhalmozódott elektronok, elkezdenek az ellenálláson keresztül elfolyni! Tehát a kondenzátorból rögtönzött elemünk, áramot hajt át az ellenálláson, miközben az elem (kondenzátor) lemerül. Ha az ellenállás nagy, és kicsi áram folyik ki a kondenzátorból, akkor ez a folyamat olyan sokáig tart, hogy közben a dióda bemenetén újra megfordul a feszültség iránya, és ismét töltődni kezd a kondenzátor a diódán keresztül. Ha lerajzoljuk az R1 ellenálláson eső feszültség időbeni alakulását, így néz ki:
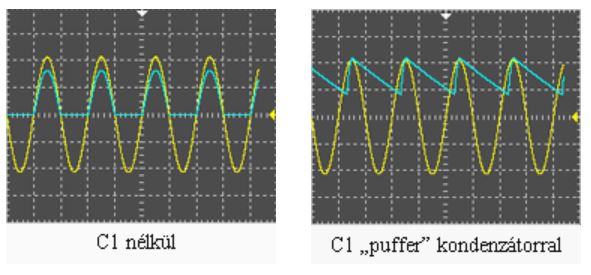
A C1 kondenzátort egy ilyen áramkörben puffer kondenzátornak hívják. Látható, hogy kondonzátor nélkül (bal oldali ábra) az ellenálláson eső feszültség az egyenirányítónál lerajzolt módon alakul (a zöld vonalt kell nézni). Ha párhuzamosan kötjük az ellenállással a kondenzátort, akkor a jobb oldali ábra szerinti az ellenállás feszültsége. Ha ide kattintasz, megtudhatod, hogyan lehet szimulátorban is előállítani a fenti ábrákat, és kísérletezhetsz kicsit a kapcsolással.
Ez a feszültség a fűrész fogaira emlékeztet, bár ha messziről nézzük, már majdnem olyan, mint egy elem, szinte állandó és folyamatos feszültséget ad. Lehet a fűrészfogasságot csökkenteni. Egyrészt növelhetjük a kapacitás nagyságát, hogy még több elektron férjen el benne, másrészt alkalmazhatunk egy több diódából készített egyenirányítót, ami a váltakozó feszültség mindkét periódusában tölti a kondenzátorunkat. Ezt Gratz hídnak hívják:
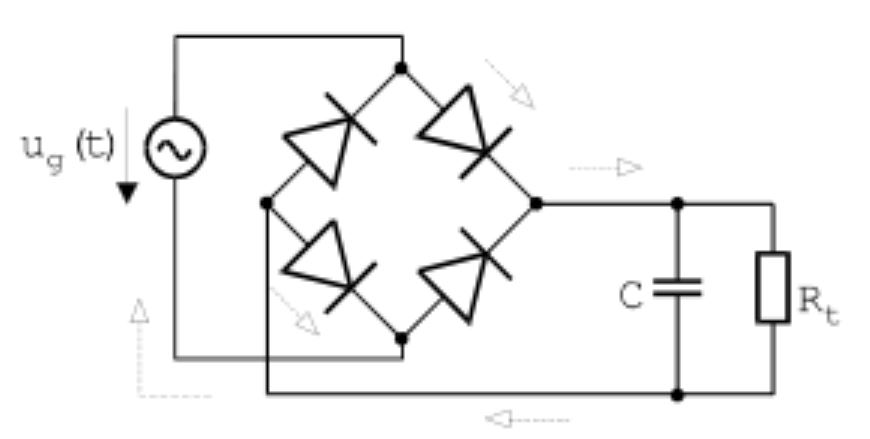
Ezen az ábrán már az egyenirányítót “meghajtó” generátort is berajzolták. Ez valójában egy 230V-ra kötött transzformátor szokott lenni. A transzformátorról később még esik szó.
Ezzel azonban még nem értünk a végére a kondenzátor alkalmazásainak. Azt látjuk, hogyan viselkedik, ha változó nagyságú feszültséget kapcsolunk rá, de nem változik meg a feszültség iránya. Ilyenkor pufferel, azaz az elektronok átmeneti tárolásával elsimítja a hullámokat. Mi történik azonban akkor, ha a kondenzátort egy olyan áramkörbe kötjük be sorosan, ahol a feszültség iránya változik. Ekkor a kondenzátor első lépésben feltöltődik elektronokkal. Nagyon rövid ideig áram folyik az áramkörben. Amikor a feszültség iránya megfordul, a kondenzátorban lévő elektronok azonnal áramlani kezdenek kifelé a kondenzátorból, hiszen pont az a feszültség pólus került a kondenzátor kivezetésére, ahová az elektronok menni szeretnének. Közben kondenzátor másik kivezetése elkezd elektronokkal megtöltődni. Ekkor a feszültség iránya újra megfordul. Most a másik kivezetésből kezdenek el kifolyni az elektronok. És megtörténik a csoda, áram folyik a vezetékben, pedig a kondenzátor szakadás, nincs fémes vezető kapcsolat a két kivezetése között. Minél több elektront tud tárolni a kondenzátor (minél nagyobb a kapacitása) annál nagyobb áram tud folyni. Ha növeljük a feszültség váltakozás frekvenciáját (szaporaságát), akkor az is növeli az átfolyó áram nagyságát, hiszen rövidebb időn belül felhasználjuk az összegyűlt elektronokat. Lássunk erre is egy alkalmazási példát:
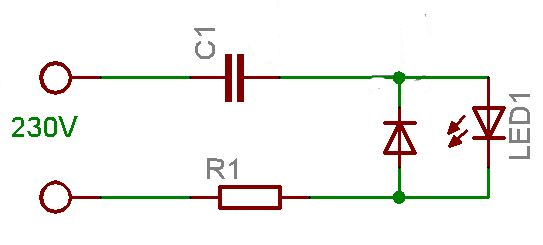
A kapcsolás a Hobbielektronika weboldalról származik. A kondenzátor és az ellenállás értékének megfelelő megválasztásával egy LED-et közvetlenül a 230V hálózati feszültségre köthetünk, és ez a kis áramkör, jelzi, ha van feszültség a konnektorban. Megépítését kezdőknek nem ajánlom, a 230V feszültség életveszélyes.
Azonban a kondenzátor soros bekötését érdemes a szimulátorban megvizsgálni. Különösen izgalmas eredményeket kaphatunk, ha megvizsgáljuk mi történik ha a frekvenciát, a kapacitás értékét, vagy az ellenállás értékét változtatjuk. Az eredményre a kapcsolás bemenő feszültségének jelalakja is hatással van. Szimulátorban szinusz, négyszög és unipoláris négyszög jelalakkal is kísérletezgettem!
Összefoglalva: a kondenzátor egy olyan alkatrész, ami egyen feszültség esetén szakadásként viselkedik, ekkor a “pufferelési” feszültség simító képességét használhatjuk fel. Váltakozó feszültség hatására már nem szakadás, hanem a frekvencia növekedésével egyre jobban vezetővé válik, nagy frekvencián rövidzárként viselkedik. Ezt a tulajdonságát az egyenfeszültség leválasztására, és a váltakozó feszültség átengedésére használjuk fel. Ilyen leválasztó kondenzátort találunk a hangerősítők bemenetén. Különböző feszültségen üzemelő eszközöket (pl. mp3 lejátszó, aktív hangfal) kapcsolhatunk össze vezetékkel, nem zavarják egymást, mert a leválasztó kondenzátoron csak a hang megy át. Persze ehhez tudni kell, hogy a hangok rezgésekből állnak, és ezeknek a rezgéseknek a frekvenciája kb 50-20.000Hz frekvenciájú. A Hz (Hertz) a frekvencia mértékegysége, és pl. a 20.000 Hz az másodpercenként 20.000 rezgést, feszültség irány változást jelent. Pl. a konnektorban a hálózati feszültség másodpercenként 50-szer változik meg, tehát 50Hz a frekvenciája. A mobiltelefonunk rádióhullámokkal közvetiti a hangunkat, ennek frekvenciája 900Mhz-1800Mhz. A 900Mhz (megahercz) 900 millió rezgést jelent másodpercenként.
Tekercs:
Ritkán szerepel amatőr elektronikai kacsolásokban tekercs, de meg kell említeni, mert egyes kapcsolásokban láthatunk ilyet is. A tekercs egy vas alapanyagú rudra, vagy gyűrűre feltekert drót. Nagyon nagy frekvenciával dolgozó áramkörökben nincs is vasmag a tekercsben, csak úgy a levelgőben tekeredik. Áramköri jele:

Ha nincs vasmag amire a drótot tekerték, akkor az egyenes vonalat el szokták hagyni a rajzból. Ha egy tekercsre feszültséget kapcsolunk, akkor áram folyik át rajta. Ha egy vezetékben áram folyik, akkor az mágneses teret épít fel maga körül. A mágneses tér felépüléséhez energia kell. Ezt az energiát a tekercs a rajta átfolyó áramból “lopja” el. Vagyis amikor elkezd az áram átfolyni a tekercsen, akkor a mágneses tér felépüléséig a tekercs nagy ellenállást mutat, nem engedi folyni az áramot. Kis idő után már növekszik az átfolyó áram nagysága, azaz csökken a tekercs ellenállása. Idővel a tekercs rövidzárként viselkedik, hiszen drótból van. Azonban a mágneses térben tárolt energia nem vész el. Amikor megszűnik a tekercsen átfolyó áram, a mágnesen tér “összeomlik” és igyekszik fenntartani az áramot a tekercsben. Ha nem tudja az áramot fenntartani, akkor a két kivezetése között a feszültséget fogja egyre nagyobbra emelni ennek érdekében. Mire jó ez? Pont ellentéte a kondenzátornak. Az egyenáramot kis idő után átengedi magán. Ha azonban váltakozó feszültséget kapcsolunk rá, a frekvencia növekedésével a tekercs ellenállása növekedni kezd. Amikor az átfolyó áram iránya megváltozik, mindig fel kell építenie a mágneses teret, és addig nagy az ellenállása. Ha elegendően gyakran változik az áram iránya, akkor folyamatosan nagy is marad az ellenállása. Gyakorlatilag a tekercs átengedi az egyenáramot, de a váltakozó áramot elegendően nagy frekvencia esetén nem. Az, hogy milyen frekvencián reagál a tekercs, az a menetszámától, a vasmag anyagától stb. függ. A tekercs fontos fizikai jellemzője az induktivitása. Minél nagyobb egy tekercs menetszáma, annál nagyobb az induktivitása. Ha ügyesen konstruáljuk meg az elektronikai kacsolásunkat, akkor a tekercs képes feszültséget növelni, hiszen a mágneses tér összeomlásakor igyekszik fenntartani az áramot, ezt pedig csak egyre nagyobb feszültséggel tudja elérni. Példaként itt egy feszültség növelő tápegység elvi működését bemutató ábra:
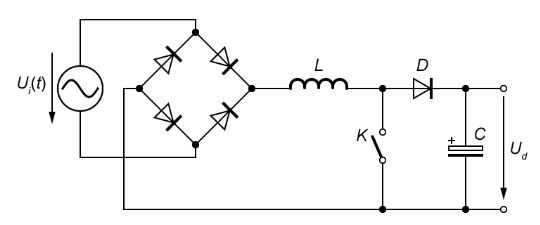
Nem kell pontosn megérteni a működést. Lényeg az, hogy amikor a kapcsolót megszakítjuk, a tekercs magára marad, és a mágneses teében tárolt energiát feszültséggé alakítja a kivezetésein, amivel rögtön egy kondenzátort tölt fel. A kapcsoló nyilván elektronikus kacsoló, mert másodpercenként több tizezer kapcsolást kell végezni. Ezek a feszültség növelő kapcsolások készen kaphatók, és sokkal bonyolultabbak. Itt láthatsz egy példát!
Transzformátor:
Ha a tekercs működését megértettük, akkor a transzformátor nagyon egyszerű lesz. Ez nem egy, hanem két tekercs, amit közös vasmagra tekercseltek. Ha az egyik tekercsben áram folyik, akkor az mágneses teret épít fel a vasmagban. Ez a mágneses tér hat a másik tekercsre is. Pontosabban a mágneses tér változása van hatással a tekercsre, mert amikor a mágneses tér felépül vagy éppen összeomlik, a másik tekercsben is feszültséget indukál. Ez a feszültség függ a menetszámtól. Ha a két tekercs menetszáma megegyezik, akkor pont akkora feszültséget kapunk a második tekercsben, mint amekkorát az első tekercsre kapcsoltunk. A szerepük alapján a tekercseknek nevet is adtak, az amire feszültséget kapcsolunk, az a primer tekercs, amiben indukálódik a feszültség, az a szekunder tekercs. Nagyon jó magyarázó ábrát találtam a regi.tankonyvtar.hu weboldalon:
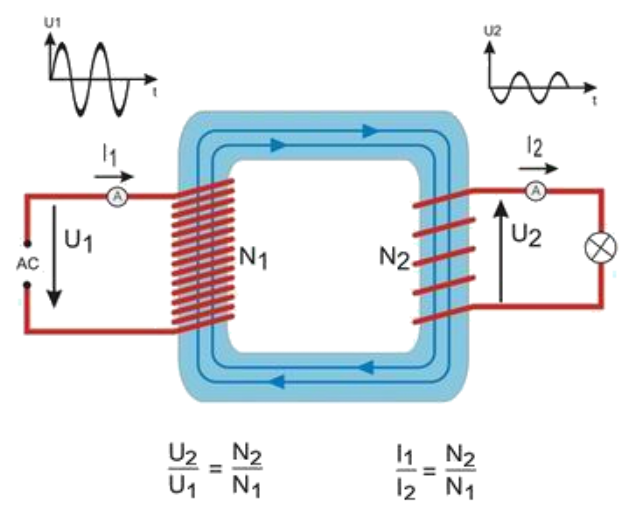
Sok helyen használunk transzformátort. Az elektronikai amatőrök leginkább tápegységeket építenek a segítségével. 230V feszültséget rákapcsoljuk a primer tekercsre, a szekunder tekercsen pedig egy sokkal kisebb feszültséget kapunk. Azt, hogy mekkora a szekunder feszültség, azt a transzformátor gyártója dönti el. Olyat kell venni, ami nekünk jó. Leggyakrabban 9V és 15V feszültségűt használtam eddig. Fontos jellemzője a transzformátornak, hogy mekkora áramot tud biztosítani a szekunder tekercs. Ez persze a transzformátor teljesítményétől függ. Erről még nem esett szó. A teljesítmény összefügg az elektromos berendezés áramfelvételével. Minél nagyobb egy berendezés teljesítménye, annál nagyobb áramot fogyaszt. Egy elektromos fűtőtest 8-10A áramot is elfogyaszt a konnektorunkból. Egy kvarcóra évekig működik egy 1,5V-os gombelemről, sejthető, hogy az áramfelvétele az amper milliomod része körül lehet. A teljesítmény a feszültség és az áram szorzata:
P = U * I
A teljesítmény jele a P, mértékegysége a Watt (W). Ez az összefüggés igaz a transzformátorra is. Ha 12V váltakozó feszültségre van szükségünk, és 1A áramot fogyaszt az áramkörünk, akkor a transzformátor 12V*1A=12W. Illik felültervezni, ebben az esetben minimum 20W-os transzformátort vegyél, különben melegedni fog, és az elektronikának a nagy meleg nem tesz jót. Mi történik akkor, ha a transzformátor szekunder tekercsére kapcsolt fogyasztó nagyobb áramot vesz fel, mint amit a transzformátor képes leadni? Egyszerű, mivel a transzformátor nem tud nagyobb teljesítményt leadni, elkezd csökkenni a kimenő feszültség. Pl. ha a 12W-os transzformátorunkból 2A áramot folyatunk ki, a feszültsége már csak 6V lesz. Ez az elmélet. Gyakorlatban valóban csökken a feszültség, és előbb utóbb a transzformátorunk tönkremegy.
Nézzünk most meg egy egyszerű tápegységet:
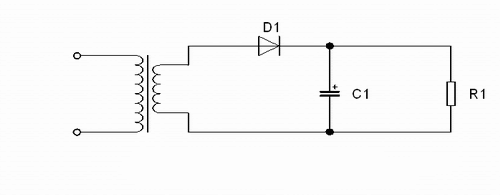
Ebben a kapcsolásban már minden alkatrészt ismerünk. A transzformátor balról az első alkatrész. A 230V-os feszültségből csinál valamilyen nagyon kicsi feszültséget, mondjuk 5V-ot. Ez azonban 5V váltakozó feszültség, és nem egyenfeszültség, ezért egyenirányítjuk egy diódával. A dióda a váltakozó feszültségnek csak az egyik felét engedi át. Ez a pulzáló feszültség töltöget egy kondenzátort, és ez elsimítja a tápegységünk kimenő feszültségét. Az R1 terhelő ellenállás jelképezi a tápegységre kapcsolt fogyasztót. Ez a tápegység a gyakorlatban nem túl jól működik. Nézzük először a kimenő feszültségét. Még nem esett szó arról, hogy az 5V váltakozó feszültség az nem is 5V. Valójában állandóan változik a feszültség. Az 5V feszültség egy átlagos érték, logikus módon azt adják meg a váltakozó feszültség esetén, ami azonos az egyenáram munkavégző képességével (effektív értékkel).
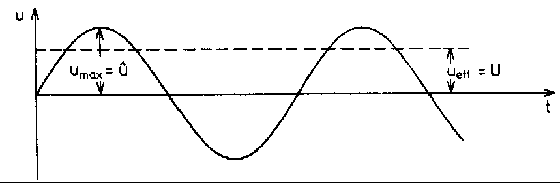
Az ábrán a hálózati feszültség időbeni változását látjuk. Az “Ueff”-el (effektív feszültség) jelölt feszültséget használjuk a váltakozó feszültség jellemzésére. A feszültség lehetséges maximális értéke ennek kb. 1,41 szerese. Egy AC 5V esetén a csúcsérték kb 7V. Ezt feszültséget kapcsoljuk a kondenzátorra, így az fel is töltődik 7V feszültségre. Képzeletbeli tápegységünk tehát nem 5,hanem 7V-os. Azért sem ideális tápegység, mert ha csökkentjük az R1 ellenállás értékét, egyre nagyobb áramot veszünk ki a tápegységből, növekedni fog a kimenő feszültség fűrészfogassága, hiszen amikor a dióda éppen nincs nyitva és nem tölti a kondenzátort, akkor a kondenzátor merül, és csökken a feszültsége. Ha nem kapcsolunk terhelő ellenállást a kimenetre, akkor nagyon szép folyamatos 7V feszültséget kapunk, de ilyen eset nincs, hiszen valamit táplálni akarunk árammal, ezért csináljuk a tápegységet. A helyzet még ennél is rosszabb. Ha csökkentjük a terhelő ellenállást és nő az áramfelvétel, a transzformátorunk is elkezdi csökkenteni a feszültségét. Azt tapasztaljuk, hogy a 7V is csökkenni fog. És még nincs vége. Ha ezt a tápegységet véletlenül rövidre zárjuk, azaz az R1 ellenállás véletlenül 0 ohm közelébe kerül, a dióda szinte azonnal tönkremegy. Tápegységünk nem védett az emberi hibák ellen. Van megoldás, remek áramköröket kaphatunk készen, melyek stabil és pontos feszültséget állítanak elő egy kicsivel nagyobb bemenő feszültségből. A segédeszközökről szóló részekben találhatsz erre is példát. Ennek a tápegységnek kicsit más a működési elve, úgynevezett kapcsolóüzemű tápegység (ára kb. 400Ft).
Tranzisztor:
Lassan elérkezünk az izgalmasabb alkatrészekhez. A tranzisztor olyan eszköz amivel elektromos jeleket tudunk felerősíteni. Alapeleme pl. a HIFI erősítőknek. Azonban én most inkább a digitális felhasználására szeretnék koncentrálni. Tegyük fel, hogy van egy feszültség kimenetünk valahol az áramköreinkben, amivel szeretnénk egy LED-et meghajtani. Jó lenne, ha a LED világítana, de a feszültség jelünk túl kicsi teljesítményű. Ha rákötjük a LED-et, az egyáltalán nem világit. Pl. azért, mert a feszültség jelünk nagysága 1V, és a LED-nek legalább 2-2,5V feszültség kell, hogy világítson. Gyorsan vegyünk egy tranzisztort, mert az segíteni fog megoldani a problémát. Áramköri jelei:
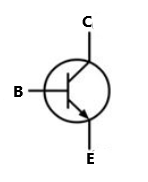
Ha egy LED bekapcsolására akarjuk használni, akkor a következő áramkört kell megépítenünk.:
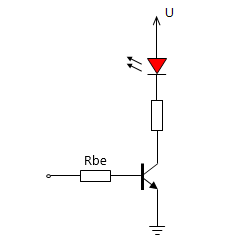
Ennek az áramkörnek az U betűvel jelölt ponton tápfeszültséget kell adnunk, ami nagyobb kell, hogy legyen, mint a LED nyitófeszültsége. Legyen pl. 5V. Alul a tranzisztor egyik kivezetésénél az a három vonallal csíkozott nyíl a tápfeszültség negatív pólusát jelenti, így is szokták jelölni. Kis kapcsolásunkban a tranzisztor bemenetére egy soros ellenállást kapcsoltunk Rbe jelöléssel. Erre azért van szükség, mert a tranzisztor valójában nem feszültséggel, hanem árammal vezérelhető. A bemenetére kapcsolt feszültség hatására a soros ellenálláson keresztül áram folyik a tranzisztor nyíllal jelölt kivezetésén keresztül a tápegység negatív pólusa felé. Könnyebb megérteni, hogy mi történik, ha lerajzoljuk a tranzisztor belső felépítését, ami valójában két szembe kapcsolt dióda.
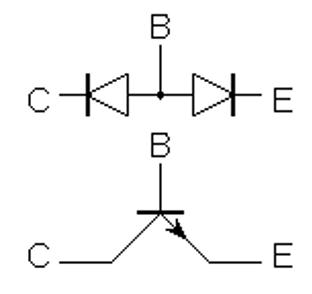
Ha két diódát úgy rakunk össze, ahogy láthatjuk az ábrán, akkor ezeken biztosan nem fog áram átfolyni a C és az E jelű kivezetéseken keresztül. Valamelyik dióda mindig zárva lesz. Azonban valahogyan rávehetnénk az egyik diódát, hogy nyisson ki, és akkor már a másikon is átfolyna az áram. Pl. erre jó lehetőség, hogy a B kivezetésre legalább 0,7V pozitív feszültséget kapcsolunk az E kivezetéshez képest. Ekkor a B és E közötti dióda kinyit. Áram folyik rajta. Ekkor viszont már a másik diódán is folyhat áram, hiszen az eleve nyitó irányban van, ha a C kivezetésre pozitív feszültséget kapcsoltunk az E-hez képest.
Talán így már érthető a kapcsolás működése. A bemenetre kicsivel nagyobb feszültséget kell kapcsolni mint egy dióda nyitófeszültsége, ekkor az ellenálláson keresztül áram folyik a tranzisztorba a B kivezetésén keresztül, ez kinyitja a diódát. Itt nagyon kicsi áramokról beszélünk. Ha azonban a dióda kinyitott, megindul az áram a C és E kivezetés között. Ott az áram nagyságát a kapcsolásban elhelyezett ellenállás határozza meg, ami jelen esetben egy soros ellenállás LED kapcsolás, tehát kb. 150Ω ellenállással 20 mA lehet. Ez nem teljesen igaz, mert a tranzisztor B kivezetésén befolyó és a C kivezetésen befolyó áram nem teljesen független egymástól. Van a tranzisztornak egy nagyon fontos paramétere, az erősítése, ami meghatározza, hogy a B kivezetésen befolyó áram hatására mennyi lesz a C kivezetésen befolyó áram nagysága. Pl. ha a tranzisztor erősítése 1000, az azt jelenti, hogy a B kivezetésen befolyó 0,02mA hatására a C kivezetésen 20mA áram folyik. Egy átlagos tranzisztor 200-1000 erősítéssel rendelkezik típustól függően. Ha ismerjük az erősítést, akkor a bemenő ellenállás is ki tudjuk számítani. Ha a bemenetre 1V feszültséget kapcsolunk, akkor a dióda nyitó feszültsége miatt 1V-0,7V=0,3V feszültség hatására 0,02mA áramnak kell folynia. Tehát az ellenállás 0,3V/0,02mA=15KΩ. Egy valós áramkörben ennél jóval kisebb ellenállást tennék oda, mert akkor a tranzisztor biztosan kinyit, nem fordulhat elő, hogy ha az adott példány gyártásakor az erősítése mondjuk 800 és nem ezer, akkor a LED halványabban világít, mert a bemenő áram hatására nem folyhat a maximális áram a LED-en.
Sokat hivatkoztam a tranzisztor kivezetéseire. Mindnek van neve: B=Bázis, C=kollektor, E=Emitter.
Ezt a kapcsolást is megépítettem a szimulátorban. Könnyebben megérthető a működés, ha változtatod a tranzisztor erősítését, a B kivezetéssel sorba kötött bázis ellenállás értékét, és a C kivezetésre kötött kollektor ellenállás értékét. Sokat lehet még tanulni abból az esetből is, amikor egy kapcsolót kötsz a tranzisztor bázisára, és megpróbálod „vezérelni” a tranzisztor B kivezetésének bázis áramát. Ebből kiderül, hogy milyen más jelenségek befolyásolják még a tranzisztor működését.
Még nem említettem még, de tranzisztorból alapvetően kétféle típus van pnp és npn típusú. Mi az előző kapcsolásokban npn típusút láthattunk. A pnp típus abban különbözik, hogy fordított feszültségeken működik, mert a benne lévő diódák is fordítva vannak bekötve. Alábbi képen látható, hogyan is néz ki egy átlagos tranzisztor (típust is írt az ábra készítője):
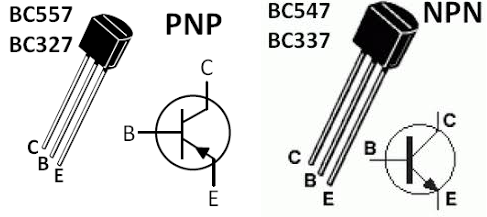
A tranzisztor segítségével nagyon kicsi vezérlő feszültség és áram felhasználásával meglehetősen nagy fogyasztót tudtunk ki és bekapcsolni. Nem foglalkoztunk vele, de a tranzisztor nem csak digitális (ki és bekapcsol) dolgokra használható. A hangerősítőkben, ahol a hangszóró membránját kell elég nagy energiával mozgatni, analóg módon használjuk. Vagyis a jelszinteket erősítünk vele. Ezek az áramkörök is nagyon érdekesek, de ezekkel most ne foglalkozzunk, bonyolultabb számítások kellenek ezeknek az áramköröknek a tervezéséhez, és megérteni is nehezebb a működésüket.
MOSFET tranzisztor:
A most következő alkatrész nagyon hasonló dologra használható mint a tranzisztor, csak teljesen másként működik, és digitális célokra sokkal jobb annál. Áramköri jele:
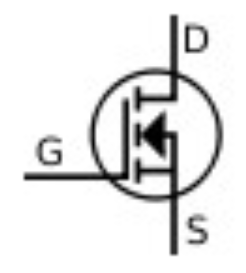
Kicsit bonyolultabbnak néz ki, de szinte ugyanúgy kell bekötni. A kivezetéseinek is más az elnevezése. A MOSFET tranzisztoroknak nagyon sok fajtája van, de amatőr áramkörök építéséhez elég ha egyet megértünk. Az előző LED meghajtó áramkör tranzisztor helyett MOSFET-el így néz ki:
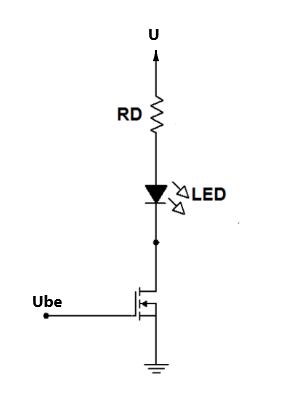
Egyetlen különbség, hogy a bemeneten nincs soros ellenállás. Azért nincs mert nem kell. A MOSFET tranzisztor valóban feszültséggel vezérelhető és nem árammal. A vezérlő bemenetet G=Gate-nek hívjuk, ami valóban egy kapu. Kinyitja a D=Drain és az S=Source kivezetések közötti átmenetet és szabadon folyhat az áram. Teljesen másként működik mint a hagyományos tranzisztor. A bemenő feszültség általában 3-5V között kell legyen ahhoz, hogy a MOSFET tranzisztor vezetni kezdjen (kinyisson). Azonban áram nem folyik befelé a bemeneten. Sokféle típust gyártanak. Egy átlagos MOSFET 30-60V feszültséget visel el a D és S között, de az átfolyó áram 10-20A (nem tévedés, amper) vagy ennél sokkal nagyobb is lehet. Nyitott állapotban a D és S között 0,05Ω (50 miliΩ) körüli az ellenállás. Természetesen ezt a kapcsolást is összeállítottam szimulátorban.
A MOSFET annyira jól használható eszköz, hogy az integrált áramkörökben is hasonló működésű alkatrészeket alkalmaznak. Rendkívül kicsi áramfelvételű áramköröket lehet így gyártani, mivel a bemenet vezérléséhez nem kell áram. Zárt állapotban a tranzisztoron sem folyik áram. A korszerű áramkörök elemekről évekig működhetnek!
Relé:
A régi korok letűnőben lévő emléke a relé, de néha még ma is egyszerűbb relét használni, mint pl. MOSFET tranzisztorral kapcsolni a nagy fogyasztókat. Főleg akkor jön jól egy relé, ha pl. háztartási gépeket kell bekapcsolni. A relé nem más, mint egy elektromágneses szerkezet, ami a tekercsen átfolyó áram hatására meghúz egy kapcsolót, ami a villanykapcsolóhoz hasonló módon bekapcsolja a rákötött fogyasztót. Az alábbi kép a vilaglexikon.hu oldalról származik, megtetszett mert szép színes:
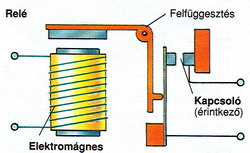
Áramköri jele valami ehhez hasonló szokott lenni:

A relé meghúzásához elég nagy áramra van szükség, még a picike áramkörbe ültethető kisméretű is legalább 50-100mA áramot igényel, ezért nem köthető közvetlenül egy átlagos mikrovezérlő vagy hasonló kis teljesítményű áramkör kimenetére. Nézzünk is meg ezért egy tranzisztorral meghajtott kapcsolást.
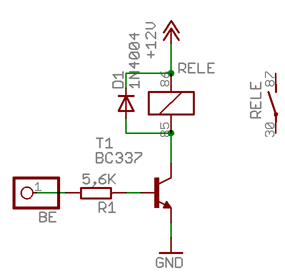
Az ábra a hobbyelektronika.hu oldalról származik. Tanúságos kapcsolás. Megadták a meghajtó tranzisztor típusát (BC337), ami egy gyakran használt típus. Az erősítése 100 és 600 közötti. A valós tranzisztorok erősítését az is befolyásolja, hogy éppen mekkora áram folyik a kollektor emitter között, azért adtak meg ilyen tág határokat. A bemenő feszültség nyilván 5V, és ehhez számították ki a bemenő ellenállást 5,6KΩ-ra. Nem ennyi jött ki a számításból, hanem egy közeli értéket választottak az olcsón kapható ellenállás értékek közül. Ezzel az ellenállással a bemenő áram (4,3V/5,6Kohm) kb 0,7mA. Ha az erősítés 100, akkor is folyhat a relén keresztül 70mA, ami jelen esetben biztosan elég, mert 50mA-nél már meghúz a relénk. Soros ellenállás nem is kell, mert a relé saját 60 ohm körüli ellenállása erre a célra pont jó. De minek a dióda?
A relé valójában egy tekercs. Amikor lekapcsoljuk róla a feszültséget, hirtelen megnövekszik a kivezetésein a feszültség. Ez olyan nagy is lehet, hogy tönkreteszi a tranzisztort. Ezért a relé tekercseivel párhuzamosan egy diódát szoktak kapcsolni záró irányban. A lekapcsoláskor keletkező feszültség fordított, tehát kinyitja a diódát, ami rövidre zárja a keletkező impulzust és elvezeti. Egy rövid pillanatra egy átlagos dióda 5-10 A áramot is elvisel, ez itt pont elég. Jobban megérthető a dióda szerepe, ha szimulátorban vizsgálod meg a tekercs önindukciós feszültégének hatását.
Egy relé kapcsoló kivezetéseire azt kötünk, amit akarunk. A bekapcsolt fogyasztónak semmilyen hatása nem lesz a relét meghajtó elektronikus áramkörökre, „leválasztottuk” azokat a későbbi áramkörökről vagy nagy teljesítményű fogyasztókról. Én pl. szivattyút kapcsoltam vele. Kapható készen olyan relé-s áramkör, amiben úgynevezett optocsatolót építettek be. Az áramkör bemenete egy LED, amikor világítani kezd, egy fényre érzékeny tranzisztor (mert ilyen is van) bekapcsolja a relét. Ennek a megoldásnak az előnye, hogy teljesen leválasztja a vezérlő áramkört a reléről, aminek a feszültség visszahatása (amit a diódával védtünk ki ebben a kapcsolásban) biztosan nem zavarhatja meg az áramkörök működését. Ez így együtt tuti megoldás. Az optocsatolónak van még egy lényeges zavarvédő hatása. Ha nagyon-nagyon hosszú vezeték köti össze a relét meghajtó kis tranzisztoros áramkörünket a vezérlő elektronikával, akkor biztosan nem keletkeznek akaratlan bekapcsolások a vezetékben keletkező zavarjelek hatására. Pl. az Arduino vezérlőnk bent van az üzemépületben, és a víz szivattyút, egy 100m-es távolságban lévő aknában kell indítani. A 100m-es vezetékben már komoly több voltos zavarjelek keletkezhetnek. Ezeknek ugyan nagyon kicsi az energiája, de mint láttuk, egy tranzisztor bázisán nagyon kicsi áramok is elegendők lehetnek a relé bekapcsolásához. Azonban az optocsatolóban elhelyezett LED ezeknek a pici áramoknak a hatására nem fog világítani, mert ahhoz nincs elég teljesítmény a zavarjelben. A lelkes amatőrök – így jómagam is – sokszor elfeledkeznek arról, hogy a valóságban már egy lakáson belül is hosszúnak számító vezetékek találhatók. A hosszú vezetékben mindig lesz zavarjel, és ha ennek kiszűrésére nem gondolunk, a pár centis vezetékkel még jól működő áramkörünk beépítés után rövid időn belül akár tönkre is mehet.
Ezzel a fejezettel az volt a célom, hogy a digitális áramkörök építéséhez és megértéséhez adjak kis segítséget. Ezért csak azokkal az alkatrészekkel foglalkoztam, melyek egy átlagos amatőr digitális kapcsolásban előfordulnak. Nem foglalkoztam az analóg áramkörökkel, és bonyolult áramkörök további lehetséges alkatrészeivel. Aki most tanul, annak nem javaslom, hogy rögtön űrhajó építésbe kezdjen. Használja azokat az alkatrészeket, amiket itt megismert. Egy két gyakorlati áramkör megépítése után jöhetnek a bonyolult dolgok. Egy Arduino áramkörrel történő ismerkedéshez, azonban ennyi bőven elegendő. Még akkor is lehet sikereket elérni, ha az itt leírtak sem voltak teljesen világosak.
Ha úgy érzed, a programozás területén is van még tanulnivalód, akkor olvasd el a kezdő programozóknak szánt ismertető anyagot is. Néhány egyszerű mintapéldával megtanulhatod a C++ nyelv alapjait, pont annyit, amennyi az Arduino programozáshoz feltétlenül szükséges.
Hajrá!